练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，平面直角坐标系中，⊙O1过原点O，且⊙O1与⊙O2相外切，圆心O1与O2在x轴正半轴上，⊙O1的半径O1P1、⊙O2的半径O2P2都与x轴垂直，且点P1、P2在反比例函数（x>0）的图象上，则　　 　　．


          

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，边长为4的等边△ABC中，DE为中位线，则四边形BCED的面积为（    ）

    A.2          B.3          C.4         D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：


             

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面中，下列命题为真命题的是（      ）

    A．四边相等的四边形是正方形     B．四个角相等的四边形是矩形

    C．对角线相等的四边形是菱形     D．对角线互相垂直的四边形是平行四边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果，则的取值范围为      .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    (x－3)2＋4x(x－3)＝0.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系中，抛物线与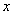轴交于A、B两点（点A在点B的左侧），与轴交于点C，点B的坐标为（3,0），将直线沿轴向上平移3个单位长度后恰好经过B、C两点。

    （1）求直线BC及抛物线的解析式；

    （2）设抛物线的顶点为D，点P在抛物线的对称轴上，且，求点P的坐标。

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，河堤横断面迎水坡AB的坡度是1∶，堤坝高BC＝5m，则坡面AB的长度

    是         m．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某黄金珠宝商店，今年4月份以前，每天的进货量与销售量均为1000克，进入4月份后，每天的进货量保持不变，因国际金价大跌走熊，市场需求量不断增加.如图1是4月前后一段时期库存量(克)与销售时间(月份)之间的函数图象. （4月份以30天计算）

    （1）该商店     月份开始出现供不应求的现象,4月份的平均日销售量为     克？

    （2）为满足市场需求，商店准备投资20万元同时购进A、B两种新黄金产品。其中购买A、B两种新黄金产品所投资的金额与销售收入存在如图2所示的函数对应关系. 请你判断商店这次投资能否盈利？

    （3）在（2）的其他条件不变的情况下，商店准备投资m万元同时购进A、B两种新黄金产品，并实现最大盈利3.2万元，请求出m的值．（利润=销售收入-投资金额）

    商品名称

    金 额

    A

    B

    投资金额x（万元）

    x

    5

    x

    1

    5

    销售收入y（万元）

    y1=kx

    (k≠0)

    3

    y2=ax2+bx

    (a≠0)

    2.8

    10

    图2
     


    查看答案和解析>>

    同步练习册答案