
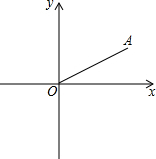
 如图,在平面直角坐标系中,点A坐标为(2,1),连接OA,点P是x轴上的一动点,如果△OAP是等腰三角形,请你写出符合条件的点P坐标P1(4,0),P2($\sqrt{5}$,0),P3(-$\sqrt{5}$,0),P4($\frac{5}{4}$,0).
如图,在平面直角坐标系中,点A坐标为(2,1),连接OA,点P是x轴上的一动点,如果△OAP是等腰三角形,请你写出符合条件的点P坐标P1(4,0),P2($\sqrt{5}$,0),P3(-$\sqrt{5}$,0),P4($\frac{5}{4}$,0). 分析 设P(x,0),再分OA=AP,OA=OP及AP=OP三种情况进行讨论.
解答 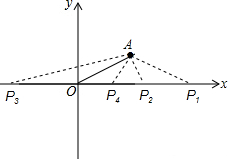 解:设P(x,0),
解:设P(x,0),
当OA=AP时,∵A(2,1),∴P1(4,0);
当OA=OP时,∵A(2,1),
∴OA=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴P2($\sqrt{5}$,0),P3(-$\sqrt{5}$,0);
当AP=OP时,∵P(x,0),(2,1),
∴(2-x)2+12=x2,解得x=$\frac{5}{4}$,
∴P4($\frac{5}{4}$,0).
综上所述,P点坐标为:P1(4,0),P2($\sqrt{5}$,0),P3(-$\sqrt{5}$,0),P4($\frac{5}{4}$,0).
故答案为:P1(4,0),P2($\sqrt{5}$,0),P3(-$\sqrt{5}$,0),P4($\frac{5}{4}$,0).
点评 本题考查的是等腰三角形的判定,在解答此题时要注意进行分类讨论,不要漏解.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:选择题
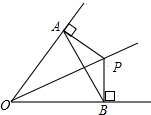 如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )
如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )| A. | PA=PB | B. | OA=OB | C. | PO平分∠APB | D. | AB垂直平分OP |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )| A. | 18 | B. | 28 | C. | 36 | D. | 46 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月租费(元) | 计费方式(元/分) | |
| A方式 | 0 | 0.05 |
| B方式 | 54 | 0.02 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com