Question

4．解下列不等式（组）：
（1）3（1-x）＞2（x+9）-5（解集在数轴上表示出来）
（2）$\left\{{\begin{array}{l}2x-6＜5x\\ \frac{x-2}{2}≤\frac{x}{3}\end{array}}\right.$．

Answer 1

分析 （1）去括号，移项，合并同类项，系数化成1即可；
（2）求出每个不等式的解集，再根据找不等式组解集的规律求出不等式组的解集即可．

解答 解：（1）3（1-x）＞2（x+9）-5，
3-3x＞2x+18-5，
-3x-2x＞18-5-3，
-5x＞10，
x＜-2，
在数轴上表示不等式的解集为：；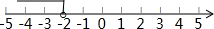

（2）$\left\{\begin{array}{l}{2x-6＜5x①}\\{\frac{x-2}{2}≤\frac{x}{3}②}\end{array}\right.$
∵解不等式①得：x＞-2，
解不等式②得：x≤6，
∴不等式组的解集为-2＜x≤6．

点评 本题考查了解一元一次不等式，解一元一次不等式组，在数轴上表示不等式的解集的应用，能正确运用不等式的基本性质求出不等式的解集是解此题的关键，难度适中．