
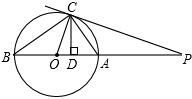
 如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC,BC,OC,那么下列结论:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.
如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC,BC,OC,那么下列结论:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③. 分析 ①证明△PBC∽△PCA,即可得到结论,这实际上是圆的切割线定理,正确;
②根据切线的性质定理,得OC⊥PC,求出△OCD∽△OPC,得出比例式即可,正确;
③根据相似三角形的性质得出比例式,即可得出答案,正确;
④证△BDC∽△CDA,即可得出答案,错误.
解答 解:①∵PC与⊙O相切于点C,
∴∠PCB=∠A,∠P=∠P,
∴△PBC∽△PCA,
∴PC2=PA•PB;
②∵OC⊥PC,PC切⊙O于C,
∴∠PCO=∠CDO=90°,
∵∠COD=∠POC,
∴△OCD∽△OPC,
∴$\frac{PC}{CD}$=$\frac{OC}{OP}$,
∴PC•OC=OP•CD;
③∵△OCD∽△OPC,
∴$\frac{OC}{OD}$=$\frac{OP}{OC}$,
∴OC2=OD•OP,
∵OA=OC,
∴OA2=OD•OP;
④∵AB为直径,
∴∠BCA=90°,
∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠B+∠BCD=∠BCD+∠ACD=90°,
∴∠B=∠ACD,
∴△BDC∽△CDA,
∴$\frac{CD}{AD}$=$\frac{BD}{CD}$,
∴CD2=BD•AD,
∴①②③正确;④错误;
故答案为:①②③.
点评 本题考查了切线的性质,相似三角形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:圆的切线垂直于过切点的半径.


科目:初中数学 来源: 题型:解答题
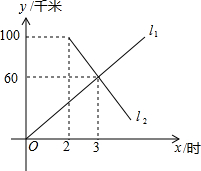 如图,A、B两地相距100千米,甲骑电动车,乙骑摩托车分别从A、B两地出发,相向而行,假设它们都保持匀速行驶,l1表示甲到A地的距离y/千米和骑车时间x/时之间的函数关系;l2表示乙到A地的距离y/千米和骑车时间x/时之间的函数关系.
如图,A、B两地相距100千米,甲骑电动车,乙骑摩托车分别从A、B两地出发,相向而行,假设它们都保持匀速行驶,l1表示甲到A地的距离y/千米和骑车时间x/时之间的函数关系;l2表示乙到A地的距离y/千米和骑车时间x/时之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
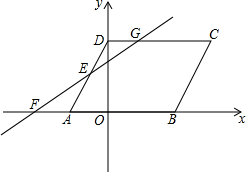 在平面直角坐标系中,O是坐标原点,平行四边形ABCD的顶点A的坐标为(-2,0),点D的坐标为(0,2$\sqrt{3}$),且AB:AD=3:2,点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线与x轴交于点F(-4,0),与DC交于点G.
在平面直角坐标系中,O是坐标原点,平行四边形ABCD的顶点A的坐标为(-2,0),点D的坐标为(0,2$\sqrt{3}$),且AB:AD=3:2,点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线与x轴交于点F(-4,0),与DC交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com