��������1��������y=ax
2+bx+c������O��A��C�����ô���ϵ�����������ߵĽ���ʽ��
��2�����ݵ������ε����ʣ�ȷ����ص�������Լ��߶γ��ȵ�������ϵ���õ�һԪ���η��̣����t��ֵ���Ӷ��ɽ⣮���ۣ����ڵ�P��
��
����ʹ���ı���ABPMΪ�������Σ�
��3�����ʹؼ�������ص��������S�ı���ʽ��Ȼ�����ö��κ����ļ�ֵ���S�����ֵ��������ṩ������������S����ʽ�ķ�������;ͬ�飬����ϸ��ζ��
����⣺��1����������y=ax
2+bx+c������O��A��C��
�ɵ�c=0����
��
���a=
-��b=
��
�������߽���ʽΪy=
-x
2+
x��
��2�����P�ĺ�����Ϊt����PN��CD�����OPN�ס�OCD���ɵ�PN=
��P��t��
�����ߵ�M���������ϣ���M��t��
-t
2+
t����
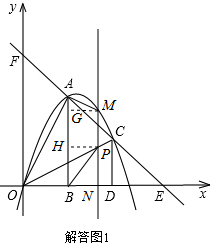
����ͼ1����M����MG��AB��G����P����PH��AB��H��
AG=y
A-y
M=2-��
-t
2+
t��=
t
2-
t+2��BH=PN=
��
��AG=BHʱ���ı���ABPMΪ�������Σ�
��
t
2-
t+2=
��
�����3t
2-8t+4=0�����t
1=2���������⣬��ȥ����t
2=
��
���P��������
��
��
����ڵ�P��
��
����ʹ���ı���ABPMΪ�������Σ�
��3������ͼ2����AOB��AC����ƽ������A��O��B�䣬A��B�佻x����T����OC��Q��A��O�佻x����K����OC��R��
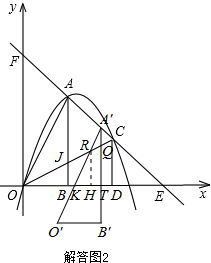
��ù�A��C��ֱ��Ϊy
AC=-x+3�������A��ĺ�����Ϊa�����A�䣨a��-a+3����
��֪��OQT�ס�OCD���ɵ�QT=
��
���Q��������a��
����
�ⷨһ��
��AB��OC�ཻ�ڵ�J��
�ߡ�A��RQ�ס�AOJ�����������ζ�Ӧ�ߵıȵ������Ʊȣ���
=
��HT=
•OB=
��1=2-a��
KT=
A��T=
��3-a����A��Q=yA��-yQ=��-a+3��-
=3-
a��

S
�ı���RKTQ=S
��A��KT-S
��A��RQ
=
KT•A��T-
A��Q•HT
=
•
•��3-a��-
•��3-
a��•��-a+2��
=
-a
2+
a-
=
-��a-
��
2+
����
-��0��
�����߶�AC�ϴ��ڵ�A�䣨
��
������ʹ�ص��������Sȡ�����ֵ�����ֵΪ
��
�ⷨ����
����R��RH��x����H�����ɡ�ORH�ס�OCD����
== ��

�ɡ�RKH�ס�A��O��B�䣬��
== ��
�ɢ٣��ڵ�KH=
OH��
OK=
OH��KT=OT-OK=a-
OH ��
�ɡ�A��KT�ס�A��O��B�䣬��
==��
��KT=
��
�ɢۣ��ܵ�
=a-
OH����OH=2a-2��RH=a-1�����Ե�R������ΪR��2a-2��a-1��
S
�ı���RKTQ=S
��QOT-S
��ROK=
•OT•QT-
•OK•RH
=
a•
a-
��1+
a-
��•��a-1��
=
-a
2+
a-
=
-��a-
��
2+
����
-��0��
�����߶�AC�ϴ��ڵ�A�䣨
��
������ʹ�ص��������Sȡ�����ֵ�����ֵΪ
��
�ⷨ����

��AB=2��OB=1����tan��O��A��B��=tan��OAB=
��
��KT=A��T•tan��O��A��B��=��-a+3��•
=
-a+
��
��OK=OT-KT=a-��
-a+
��=
a-
��
����R��RH��x����H��
��cot��OAB=tan��RKH=
=2��
��RH=2KH
�֡�tan��OAB=tan��ROH=
=
=
��
��2RH=OK+KH=
a-
+
RH��
��RH=a-1��OH=2��a-1����
���R����R��2a-2��a-1��
S
�ı���RKTQ=S
��A��KT-S
��A��RQ=
•KT•A��T-
A��Q•��x
Q-x
R��
=
•
•��3-a��-
•��3-
a��•��-a+2��
=
-a
2+
a-
=
-��a-
��
2+
����
-��0��
�����߶�AC�ϴ��ڵ�A�䣨
��
������ʹ�ص��������Sȡ�����ֵ�����ֵΪ
��









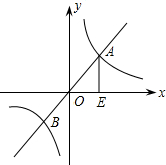 ��2012•���ݣ���ͼ����֪����y=2x�ͺ���y=
��2012•���ݣ���ͼ����֪����y=2x�ͺ���y=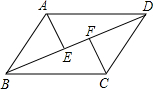 ��2012•���ݣ���ͼ����ƽ���ı���ABCD�У�E��F�ǶԽ���BD�ϵ����㣬��BE=DF������AE��CF��������룺AE��CF��������������ϵ��������IJ������֤����
��2012•���ݣ���ͼ����ƽ���ı���ABCD�У�E��F�ǶԽ���BD�ϵ����㣬��BE=DF������AE��CF��������룺AE��CF��������������ϵ��������IJ������֤����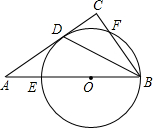 ��2012•���ݣ���ͼ����Rt��ABC�У���C=90�㣬��ABC��ƽ���߽�AC�ڵ�D����O��AB��һ�㣬��O��B��D���㣬�ҷֱ�AB��BC�ڵ�E��F��
��2012•���ݣ���ͼ����Rt��ABC�У���C=90�㣬��ABC��ƽ���߽�AC�ڵ�D����O��AB��һ�㣬��O��B��D���㣬�ҷֱ�AB��BC�ڵ�E��F�� ��2012•���ݣ���ͼ����A��B��C�ڡ�O�ϣ���ACB=30�㣬��sin��AOB��ֵ�ǣ�������
��2012•���ݣ���ͼ����A��B��C�ڡ�O�ϣ���ACB=30�㣬��sin��AOB��ֵ�ǣ�������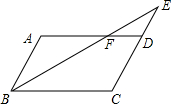 ��2012•���ݣ���ͼ��ƽ���ı���ABCD�У�E��CD���ӳ�����һ�㣬BE��AD���ڵ�F��CD=2DE������DEF�����Ϊa����ƽ���ı���ABCD�����Ϊ
��2012•���ݣ���ͼ��ƽ���ı���ABCD�У�E��CD���ӳ�����һ�㣬BE��AD���ڵ�F��CD=2DE������DEF�����Ϊa����ƽ���ı���ABCD�����Ϊ