
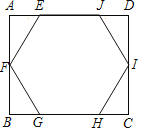
【题目】如图,在矩形ABCD中有一个正六边形EFGHIJ,其顶点均在矩形的边上,边EJ和边GH分别在矩形的边AD和BC上,则![]() =_____.
=_____.
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴分别交于
与x轴分别交于![]() ,
,![]() 两点,与y轴交于点C.
两点,与y轴交于点C.
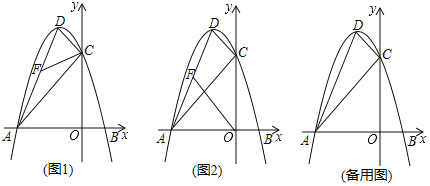
(1)求抛物线的表达式及顶点D的坐标;
(2)点F是线段AD上一个动点.
①如图1,设![]() ,当k为何值时,
,当k为何值时,![]() .
.
②如图2,以A,F,O为顶点的三角形是否与![]() 相似?若相似,求出点F的坐标;若不相似,请说明理由.
相似?若相似,求出点F的坐标;若不相似,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,并解决问题:
“整体思想”是中学数学中的一种重要思想,贯穿于中学数学的全过程,比如整体代入,整体换元,整体约减,整体求和,整体构造,…,有些问题若从局部求解,采取各个击破的方式,很难解决,而从全局着眼,整体思考,会使问题化繁为简,化难为易,复杂问题也能迎刃而解.
例:当代数式![]() 的值为7时,求代数式
的值为7时,求代数式![]() 的值.
的值.
解:因为![]() ,所以
,所以![]() .
.
所以.![]()
以上方法是典型的整体代入法.
请根据阅读材料,解决下列问题:
(1)已知![]() ,求
,求![]() 的值.
的值.
(2)我们知道方程![]() 的解是
的解是![]() ,现给出另一个方程
,现给出另一个方程![]() ,则它的解是 .
,则它的解是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
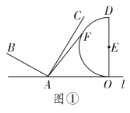
【题目】如图①,已知点![]() 、
、![]() 在直线
在直线![]() 上,且
上,且![]() 于点
于点![]() ,且
,且![]() ,以
,以![]() 为直径在
为直径在![]() 的左侧作半圆
的左侧作半圆![]() 于点
于点![]() ,且
,且![]() .
.
(1)若半圆![]() 上有一点
上有一点![]() ,则
,则![]() 的最大值为__________;
的最大值为__________;
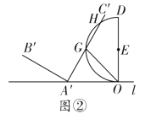
(2)向右沿直线![]() 平移
平移![]() 得到
得到![]() .
.
①如图②,若![]() 截半圆
截半圆![]() 的
的![]() 的长为
的长为![]() ,求
,求![]() 的度数;
的度数;
②当半圆![]() 与
与![]() 的边相切时,求平移距离.
的边相切时,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() x+2与x轴交于点A,与y轴交于点C,抛物线y=
x+2与x轴交于点A,与y轴交于点C,抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.

(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点;
①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1, △BCE的面积为S2, 求![]() 的最大值;
的最大值;
②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() ,过点
,过点![]() 和点
和点![]() ,与y轴交于点C,连接AC交x轴于点D,连接OA,OB
,与y轴交于点C,连接AC交x轴于点D,连接OA,OB
![]() 求抛物线
求抛物线![]() 的函数表达式;
的函数表达式;
![]() 求点D的坐标;
求点D的坐标;
![]() 的大小是______;
的大小是______;
![]() 将
将![]() 绕点O旋转,旋转后点C的对应点是点
绕点O旋转,旋转后点C的对应点是点![]() ,点D的对应点是点
,点D的对应点是点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点M,在
交于点M,在![]() 旋转过程中,当点M与点
旋转过程中,当点M与点![]() 重合时,请直接写出点M到AB的距离.
重合时,请直接写出点M到AB的距离.
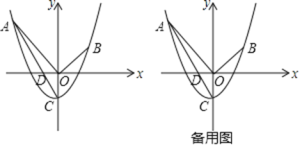
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】很多交通事故是由于超速行驶导致的,为集中治理超速现象,高速交警在距离高速路40米的地方设置了一个测速观察点,现测得测速点的西北方向有一辆小型轿车从B处沿西向正东方向行驶,2秒钟后到达测速点北偏东![]() 的方向上的C处,如图.
的方向上的C处,如图.
(1)求该小型轿车在测速过程中的平均行驶速度约是多少千米/时(精确到1千米/时)?
(参考数据:![]() )
)
(2)我国交通法规定:小轿车在高速路行驶,时速超过限定速度10%以上不到50%的处200元罚款,扣3分;时速超过限定速度50%以上不到70%的处1500元罚款,扣12分;时速超过限定时速70%以上的处1500元罚款,扣12分.若该高速路段限速120千米/时,你认为该小轿车驾驶员会受到怎样的处罚.
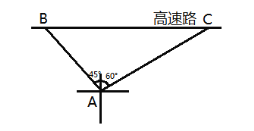
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,BC=2,E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF.
(1)求证:△ADF≌△ABE.
(2)若BE=1,求sin∠AED的值.
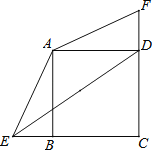
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com