练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    　　如图，∵　AB∥CD，∴　∠A+_____________=180°( _____________ )；

    　　∵　BC∥AD，∴　∠A+________=180°( ____________ )．所以∠B=∠________．

     

    答案：
    解析：

    		　　∠D　两直线平行，同旁内角互补　∠B两直线平行　同旁内角互补　∠D

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：044

    阅读下列证明过程：已知，如图四边形ABCD中，AB＝DC，AC＝BD，AD≠BC，求证：四边形ABCD是等腰梯形．

    读后完成下列各小题．

    (1)证明过程是否有错误？如有，错在第几步上，答：　　　　　　　　　　　　 　　　　　　　　　　　　 ．

    (2)作DE∥AB的目的是：　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　 ．

    (3)有人认为第9步是多余的，你的看法呢？为什么？答：　　　　　　　　　　　　　　 　　　　　　　　　　　　　　．

    (4)判断四边形ABED为平行四边形的依据是：　　　　　　　　　　　　 　　　　　　　　　　 ．

    (5)判断四边形ABCD是等腰梯形的依据是　　　　　　　　　　　　 　　　　　　　　　　　　．

    (6)若题设中没有AD≠BC，那么四边形ABCD一定是等腰梯形吗？为什么？

    答：　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　 ．

    查看答案和解析>>

    科目：初中数学 来源：初中几何同步单元练习册 第1册 题型：022

    　　如图，已知∠1＝，∠2＝，

    　　求证：AB∥CD．

    　　证明：因为　　∠1＝，∠2＝(　　)，

    　　所以　　∠1＝∠2．

    　　因为　　∠2＝∠3(　　)，

    　　所以　　∠1＝∠3(　　)．

    　　所以　　AB∥CD(　　)，

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：044

    　　如图，四边形ABCD中，AD⊥AB  BC⊥AB   BC=2AD   DE⊥CD交AB边于E，连结CE。请找出DE、AE、CE之间的等量关系并加以证明。  C　　　　　　　　

    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  

    　　　　　　　　　　　　　　　　　　　　  D

    　　　　　　　　　　　　　　　　　　　　

    　　　　　　　　　　　　　　　　　　　　  A　　　　　　　　    B

    　　　　   　　　　　　　　　　　　　　　　　E   

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    探索勾股定理时，我们发现“用不同的方式表示同一图形的面积”可以解决线段和（或差）的有关问题，这种方法称为面积法。请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC,BD为腰AC上的高。

    (1)若BD=h，M时直线BC上的任意一点，M到AB、AC的距离分别为。

    ①　　 若M在线段BC上，请你结合图形①证明：= h；　　　　　　　　　　

    ②　　 当点M在BC的延长线上时，，h之间的关系为　　　　　 （请直接写出结论，不必证明）　　　　　　　　　　　　　　　　　　　　　　　　　

    （2）如图②，在平面直角坐标系中有两条直线：y = x + 6 ； ：y = -3x+6 若上的一点M到的距离是3，请你利用以上结论求解点M的坐标。

    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 图②


    查看答案和解析>>

    科目：初中数学 来源： 题型：

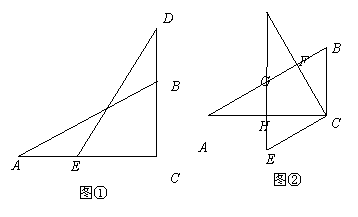
    两个大小相同且含角的三角板ABC和DEC如图①摆放，使直角顶点重合. 将图①中△DEC绕点C逆时针旋转得到图②，点F、G分别是CD、DE与AB的交点，点H是DE与AC的交点.

    （1）不添加辅助线，写出图②中所有与△BCF全等的三角形；

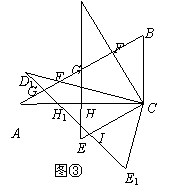
    （2）将图②中的△DEC绕点C逆时针旋转得△D1E1C，点F、G、H的对应点分别为F1、G1、H1 ，如图③.探究线段D1F1与AH1之间的数量关系，并写出推理过程；

    　　 （3）在（2）的条件下，若D1E1与CE交于点I，求证：G1I =CI.

    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D　
    D


    查看答案和解析>>

    同步练习册答案