
 的图象与
的图象与 轴相交于两个不同的点
轴相交于两个不同的点 、
、 ,与
,与 轴的交点为
轴的交点为 .设
.设 的外接圆的圆心为点
的外接圆的圆心为点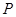 .
.
 与
与 轴的另一个交点D的坐标;
轴的另一个交点D的坐标; 恰好为
恰好为 的直径,且
的直径,且 的面积等于
的面积等于 ,求
,求 和
和 的值.
的值.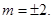
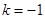
 的坐标为
的坐标为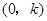
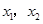 是方程
是方程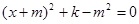 即
即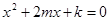 的两根,
的两根,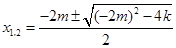 ,
,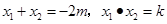
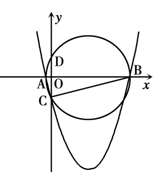
 轴的另一个交点为D,由于AB、CD是⊙P的两条相交弦,设它们的交点为点O,连结DB,
轴的另一个交点为D,由于AB、CD是⊙P的两条相交弦,设它们的交点为点O,连结DB,
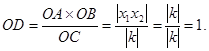
 在
在 轴的负半轴上,从而点D在
轴的负半轴上,从而点D在 轴的正半轴上,
轴的正半轴上, 的坐标为
的坐标为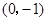 ,即
,即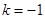
 ,
, 解得
解得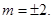


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源:不详 题型:填空题
 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = .
= . 
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与y轴突于A点,过点A的直线y=kx+l与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
与y轴突于A点,过点A的直线y=kx+l与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 的图象和性质.
的图象和性质.| x | … |  | 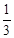 |  | 1 | 2 | 3 | 4 | … |
| y | … | | | | | | | | … |

 的最小值.
的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com