
��ͼ�����߳�Ϊ4�ĵȱ�������AOB������ƽ��ֱ������ϵxoy�У�F��AB���ϵĶ��㣨����˵�A��B�غϣ�������F�ķ��������� ��k��0��x��0����OA�߽��ڵ�E������F��FC��x���ڵ�C������EF��OF��
��k��0��x��0����OA�߽��ڵ�E������F��FC��x���ڵ�C������EF��OF��
��1����S��OCF= �����������Ľ���ʽ��
�����������Ľ���ʽ��
��2���ڣ�1���������£����ж��Ե�EΪԲ�ģ�EA��Ϊ�뾶��Բ��y���λ�ù�ϵ����˵�����ɣ�
��3��AB�����Ƿ���ڵ�F��ʹ��EF��AE�������ڣ������BF��FA��ֵ���������ڣ���˵�����ɣ�
�⣺��1����F��x��y������x��0��y��0������OC=x��CF=y��
��S��OCF= xy=
xy= ����xy=2
����xy=2 ����k=2
����k=2 ��
��
�෴������������ʽΪ ��x��0����
��x��0����
��2����Բ��y�����룬�������£�
����E��EH��x�ᣬ����ΪH������E��EG��y�ᣬ����ΪG��
�ڡ�AOB�У�OA=AB=4����AOB=��ABO=��A=60�㣬
��OH=m���� ��
��
��EH= m��OE=2m����E������m��
m��OE=2m����E������m�� m����
m����
��E�ڷ����� ͼ���ϣ���
ͼ���ϣ��� ��
��
��m1= ��m2=-
��m2=- ����ȥ����
����ȥ����
��OE=2 ��EA=4��2
��EA=4��2 ��EG=
��EG= ��
��
��4��2 ��
�� ����EA��EG��
����EA��EG��
����EΪԲ�ģ�EA��Ϊ�뾶��Բ��y�����롣
��3�����ڡ�
������ڵ�F��ʹAE��FE��
��E����EH��OB�ڵ�H����BF=x��
�ߡ�AOB�ǵȱ������Σ�
��AB=OA=OB=4����AOB=��ABO=��A=60�㡣
��BC=FB•cos��FBC= x��FC=FB•sin��FBC=
x��FC=FB•sin��FBC= x��
x��
��AF=4��x��OC=OB��BC=4�� x��
x��
��AE��FE����AE=AF•cosA=2�� x��
x��
��OE=OA��AE= x+2��
x+2��
��OH=OE•cos��AOB= x+1��EH=OE•sin��AOB=
x+1��EH=OE•sin��AOB= x+
x+ ��
��
��E�� x+1��
x+1�� x+
x+ ����F��4��
����F��4�� x��
x�� x����
x����
��E��F����˫���� ��ͼ���ϣ�
��ͼ���ϣ�
�ࣨ x+1����
x+1���� x+
x+ ��=��4��
��=��4�� x��•
x��• x����ã�x1=4��x2=
x����ã�x1=4��x2= ��
��
��BF=4ʱ��AF=0��BF��AF�����ڣ���ȥ��
��BF= ʱ��AF=
ʱ��AF= ��BF��AF=1��4
��BF��AF=1��4
���������������1����F��x��y�����õ�OC=x��CF=y����ʾ��������OCF����������xy��ֵ����Ϊk��ֵ������ȷ��������������ʽ��
��2����E��EH��ֱ��x�ᣬEG��ֱ��y�ᣬ��OHΪm�����õȱ������ε����ʼ�������Ǻ��������ʾ��EH��OE��������ʾ��E�����꣬���뷴��������ʽ�����m��ֵ��ȷ����EG��OE��EH�ij�������EA��EG�Ĵ�С��ϵ���ɶ���ԲE��y���λ�ù�ϵ�����жϡ�
��3����E��EH��ֱ��x�ᣬ��FB=x�����õȱ������ε����ʼ�������Ǻ��������ʾ��FC��BC��������ʾ��AF��OC����ʾ��AE��OE�ij����ó�OE��EH�ij�����ʾ��E��F���꣬����E��F���ڷ�����ͼ���ϣ��õ���������˻�����г����̣�������̵Ľ�õ�x��ֵ���������BF��FA�ı�ֵ����


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����������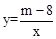 (mΪ����)��ͼ����A����1��6��.
(mΪ����)��ͼ����A����1��6��.
��1����m��ֵ��
��2����ͼ������A��ֱ��AC�뺯��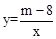 ��ͼ���ڵ�B����x�ύ�ڵ�C����AB��2BC�����C������.
��ͼ���ڵ�B����x�ύ�ڵ�C����AB��2BC�����C������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ���Ƽ�С�����ò���Χ��һ�����Ϊ60��2�ľ��οƼ�ABCD������һ��AB��ǽ��ǽ��Ϊ12������AD�ij�Ϊ������DC�ij�Ϊ������
��1��������֮��ĺ�����ϵʽ��
��2����Χ�ɾ��οƼ�ABCD�����߲����ܳ�������26��������AD��DC�ij������������������������������Χ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��ֱ�� ��˫����
��˫����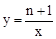 ����C��D���㣬��x�ύ�ڵ�A.
����C��D���㣬��x�ύ�ڵ�A.
��1����n��ȡֵ��Χ�͵�A�����ꣻ
��2������C��CB��y�ᣬ����ΪB����S ��ABC��4����˫���ߵĽ���ʽ��
��3���ڣ�1������2���������£���AB�� �����C�͵�D�����겢����ͼ��ֱ��д��������������ֵС��һ�κ�����ֵʱ���Ա���x��ȡֵ��Χ��
�����C�͵�D�����겢����ͼ��ֱ��д��������������ֵС��һ�κ�����ֵʱ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��������ij�ֽ�������Ҫ���в������պͶ�������������Ҫ�������յ�800�棬Ȼ��ֹͣ���ս��ж������������8minʱ�������¶Ƚ�Ϊ600�森����ʱ�¶�y���棩��ʱ��x��min����һ�κ�����ϵ������ʱ���¶�y���棩��ʱ��x��min���ɷ�����������ϵ����ͼ������֪�ò��ϳ�ʼ�¶���32�森
��1���ֱ�����������պͶ���ʱy��x�ĺ�����ϵʽ������д���Ա���x��ȡֵ��Χ��
��2�����ݹ���Ҫ�������¶ȵ���480��ʱ����ֹͣ��������ô����IJ���ʱ���ж��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ������������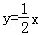 ��ͼ���뷴��������
��ͼ���뷴�������� ��k��0���ڵ�һ����ͼ����A�㣬��A����x��Ĵ��ߣ�����ΪM����֪��OAM�����Ϊ1��
��k��0���ڵ�һ����ͼ����A�㣬��A����x��Ĵ��ߣ�����ΪM����֪��OAM�����Ϊ1��
��1�����������Ľ���ʽ��
��2�����BΪ�����������ڵ�һ����ͼ���ϵĵ㣨��B���A���غϣ�����B��ĺ�����Ϊ1����x������һ��P��ʹPA+PB��С����P�����ꣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ͨ�����տư�ˣ��£��̲�һ��ϰ���̽���о�������֪����һ�κ���y=x��1��ͼ�����������������y=x��ͼ������ƽ��1����λ���ȵõ����Ƶģ����� ��ͼ�����ɷ���������
��ͼ�����ɷ��������� ��ͼ������ƽ��2����λ���ȵõ������������һ֪ʶ������⣮
��ͼ������ƽ��2����λ���ȵõ������������һ֪ʶ������⣮
��ͼ����֪���������� ��ͼ��C������������y=ax��a��0����ͼ��l�ཻ�ڵ�A��2��2���͵�B��
��ͼ��C������������y=ax��a��0����ͼ��l�ཻ�ڵ�A��2��2���͵�B��
��1��д����B�����꣬����a��ֵ��
��2�������� ��ͼ���ֱ��ABͬʱ����ƽ��n��n��0������λ���ȣ��õ���ͼ��ֱ��ΪC���l�䣬��֪ͼ��C�侭����M��2��4����
��ͼ���ֱ��ABͬʱ����ƽ��n��n��0������λ���ȣ��õ���ͼ��ֱ��ΪC���l�䣬��֪ͼ��C�侭����M��2��4����
����n��ֵ��
�ڷֱ�д��ƽ�ƺ������ͼ��C���l���Ӧ�ĺ�����ϵʽ��
��ֱ��д������ʽ �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��2011•���죩����������ֱ������ѧ��3��0��1��5�IJ�����Ƭ�����dz����ֲ�ͬ������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ������ȡһ�ţ����ÿ�Ƭ�ϵ���ѧ��Ϊ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com