
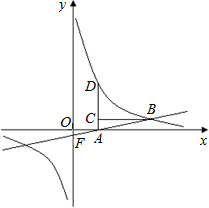
 如图,点D在双曲线上,AD垂直x轴,垂足为A,点C在AD上,CB平行于x轴交双曲线于点B,直线AB与y轴交于点F,已知AC:AD=1:3,点C的坐标为(3,2).
如图,点D在双曲线上,AD垂直x轴,垂足为A,点C在AD上,CB平行于x轴交双曲线于点B,直线AB与y轴交于点F,已知AC:AD=1:3,点C的坐标为(3,2).分析 (1)由点C的坐标为(3,2)得AC=2,而AC:AD=1:3,得到AD=6,则D点坐标为(3,6),然后利用待定系数法确定双曲线的解析式;
(2)已知A(3,0)和B(9,2),利用待定系数法确定直线AB的解析式,得到F点的坐标,然后利用三角形的面积公式计算即可
解答 解:(1)∵点C的坐标为(3,2),AD垂直x轴,
∴AC=2,
又∵AC:AD=1:3,
∴AD=6,
∴D点坐标为(3,6),
设双曲线的解析式为$y=\frac{k}{x}$
把D(2,6)代入y=$y=\frac{k}{x}$得,k=3×6=18,
所以双曲线解析式为$y=\frac{18}{x}$;
(2)设直线AB的解析式为y=kx+b,
∵CB平行于x轴交曲线于点B,
∵双曲线的解析式为$y=\frac{18}{x}$,
∴B(9,2)
把A(3,0)和B(9,2)代入y=kx+b得,3k+b=0,9k+b=2,解得$k=\frac{1}{3}$,b=-1,
∴直线AB的解析式为y=$\frac{1}{3}$x-1,
令x=0,得y=-1,
∴F点的坐标为(0,-1),
∴S△OFA=$\frac{1}{2}$×OA×OF=$\frac{1}{2}$×3×1=$\frac{3}{2}$.
点评 本题考查了利用待定系数法确定反比例函数和一次函数解析式的方法:把求解析式的问题转化为解方程或方程组.也考查了坐标与线段之间的关系以及三角形面积公式.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
 已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
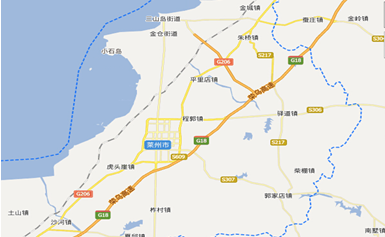
| A. | 金城镇在莱州市中心的北偏东约60°的方向上 | |
| B. | 沙河镇在莱州市中心的南偏西约45°的方向上 | |
| C. | 平里店镇在莱州市中心的南偏西约30°的方向上 | |
| D. | 柞村镇在莱州市中心的南偏东约20°的方向上 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4cm | B. | 5cm | C. | 小于4cm | D. | 不大于4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
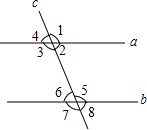 如图,直线a,b被直线c所截,现给出下列四个条件:
如图,直线a,b被直线c所截,现给出下列四个条件:| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com