
分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{2x-(x+1)(x-1)}{x-1}$÷$\frac{(x-2)^{2}}{x-1}$=$\frac{-(x-1)^{2}}{x-1}$•$\frac{x-1}{(x-2)^{2}}$=-$\frac{(x-1)^{2}}{(x-2)^{2}}$,
当x=$\sqrt{2}$+2时,原式=-$\frac{(\sqrt{2}+2-1)^{2}}{(\sqrt{2}+2-2)^{2}}$=$\frac{3+2\sqrt{2}}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:解答题
 小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远?
小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
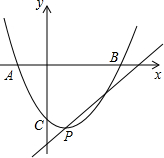 已知抛物线y=ax2-2ax+c与x轴交于A、B两点,与y轴交于点C.其中.A(-1,0),C(0,-3).
已知抛物线y=ax2-2ax+c与x轴交于A、B两点,与y轴交于点C.其中.A(-1,0),C(0,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+2y)(x-8y) | B. | (x+y)(x-16y) | C. | (-4y+x)(4y+x) | D. | (-x-4y)(x+4y) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
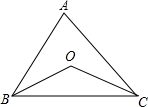 如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB,则∠BOC与∠A的大小关系是( )
如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB,则∠BOC与∠A的大小关系是( )| A. | ∠BOC=2∠A | B. | ∠BOC=90°+∠A | C. | ∠BOC=90°+$\frac{1}{2}$∠A | D. | ∠BOC=90°-$\frac{1}{2}$∠A |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 标准差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com