
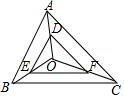
 如图,O是△ABC内任意一点,DE∥AB,DF∥AC,EF∥BC,那么△ABC与△DEF相似吗?说明理由.
如图,O是△ABC内任意一点,DE∥AB,DF∥AC,EF∥BC,那么△ABC与△DEF相似吗?说明理由. 分析 先根据DE∥AB得出△ODE∽△OAB,故$\frac{DE}{AB}$=$\frac{OD}{OA}$,同理可得$\frac{OD}{OA}$=$\frac{DF}{AC}$=$\frac{OF}{OC}$,$\frac{OF}{OC}$=$\frac{EF}{BC}$,由此可得出结论.
解答 解:△ABC∽△DEF.
理由:∵DE∥AB,
∴△ODE∽△OAB,
$\frac{DE}{AB}$=$\frac{OD}{OA}$.
同理可得$\frac{OD}{OA}$=$\frac{DF}{AC}$=$\frac{OF}{OC}$,$\frac{OF}{OC}$=$\frac{EF}{BC}$,
∴$\frac{DE}{AB}$=$\frac{DF}{AC}$=$\frac{EF}{BC}$,
∴△ABC∽△DEF.
点评 本题考查的是三角形的判定,熟知三组对应边的比相等的两个三角形相似是解答此题的关键.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
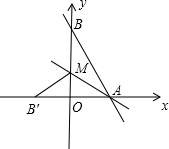 如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处.
如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
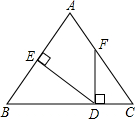 如图,△ABC中,∠A=∠B,FD⊥BC,DE⊥AB,垂足分别为D、E,∠AFD=160°.
如图,△ABC中,∠A=∠B,FD⊥BC,DE⊥AB,垂足分别为D、E,∠AFD=160°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、C的坐标分别为(0,-$\sqrt{2}$)、(2$\sqrt{2}$,0),将矩形OABC绕点O顺时针旋转45°得到矩形OA′B′C′,边A′B′与y轴交于点D,经过坐标原点的抛物线y=ax2+bx同时经过点A′、C′.
如图,在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、C的坐标分别为(0,-$\sqrt{2}$)、(2$\sqrt{2}$,0),将矩形OABC绕点O顺时针旋转45°得到矩形OA′B′C′,边A′B′与y轴交于点D,经过坐标原点的抛物线y=ax2+bx同时经过点A′、C′.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
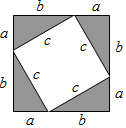 如图,大正方形的面积可以表示为(a+b)2,又可以表示为2ab+c2,由此可得等量关系a2+2ab+b2=2ab+c2,整理后可得:a2+b2=c2.
如图,大正方形的面积可以表示为(a+b)2,又可以表示为2ab+c2,由此可得等量关系a2+2ab+b2=2ab+c2,整理后可得:a2+b2=c2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com