
【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.

【答案】(1)45°;(2)12.5.
【解析】
(1)由旋转的性质得,AD=AB=10,∠ABD=45°,再由平移的性质即可得出结论;
(2)先判断出∠ADE=∠ACB,进而得出△ADE∽△ACB,得出比例式求出AE,即可得出结论.
(1)∵线段AD是由线段AB绕点A按逆时针方向旋转90°得到,
∴∠DAB=90°,AD=AB=10,
∴∠ABD=45°,
∵△EFG是△ABC沿CB方向平移得到,
∴AB∥EF,
∴∠BDF=∠ABD=45°;
(2)由平移的性质得,AE∥CG,AB∥EF,
∴∠DEA=∠DFC=∠ABC,∠ADE+∠DAB=180°,
∵∠DAB=90°,
∴∠ADE=90°,
∵∠ACB=90°,
∴∠ADE=∠ACB,
∴△ADE∽△ACB,
∴![]() ,
,
∵AB=8,AB=AD=10,
∴AE=12.5,
由平移的性质得,CG=AE=12.5.


科目:初中数学 来源: 题型:
【题目】如图,BC为Rt△ABC的斜边,∠CBA=30°,△ABD,△ACF,△BCE均为正三角形,四边形MNPE是长方形,点F在MN上,点D在NP上,若AC=2,则图中空白部分的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
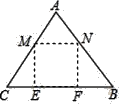
【题目】如图,王爷爷家院子里有一块三角形田地ABC,AB=AC=5米,BC=6米,现打算把它开垦出一个矩形MNFE区域种植韭菜,△AMN区域种植芹菜,△CME和△BNF区域种植青菜(开垦土地面积损耗均忽略不计),其中点M,N分别在AC,AB上,点E,F在BC上,已知韭菜每平方米收益100元,芹菜每平方米收益60元,青菜每平方米收益40元,设CM=5x米,王爷爷的蔬菜总收益为W元.
(1)当矩形MNFE恰好为正方形时,求韭菜种植区域矩形MNFE的面积.
(2)若种植韭菜的收益等于另两种蔬菜收益之和的2倍,求这时x的值.
(3)求王爷爷的蔬菜总收益为W关于x的函数表达式及W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
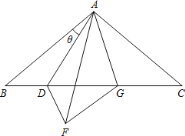
【题目】在ABC 中, AB AC , BAC=100°,点 D 在 BC 上, ABD 和AFD 关于直线 AD 对称, FAC 的平分线交 BC 于点 G,连接 FG 当BAD _________.时,DFG为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)请画出△ABC关于y轴对称的△DEF(其中D,E,F分别是A,B,C的对应点,不写画法);
(2)直接写出D,E,F三点的坐标:D( ),E( ),F( );
(3)在y轴上存在一点,使PC﹣PB最大,则点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2![]() 2x+c的顶点A在直线l:y=x
2x+c的顶点A在直线l:y=x![]() 5上.
5上.
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;
(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com