
【题目】如图1,已知抛物线的顶点坐标为(0,1)且经过点A(1,2),直线y=3x﹣4![]() 经过点B(
经过点B(![]() ,n),与y轴交点为C.
,n),与y轴交点为C.
(1)求抛物线的解析式及n的值;
(2)将直线BC绕原点O逆时针旋转45°,求旋转后的直线的解析式;
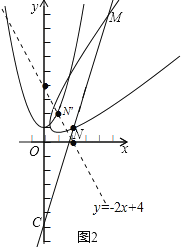
(3)如图2将抛物线绕原点O顺时针旋转45°得到新曲线,新曲线与直线BC交于点M、N,点M在点N的上方,求点N的坐标.
【答案】(1)y=x2+1,n=2![]() ;(2)y=﹣2x+4;(3)N(
;(2)y=﹣2x+4;(3)N(![]() ,
,![]() ).
).
【解析】
(1)抛物线的表达式为:y=ax2+1,将点A坐标代入上式得:2=a+1,即可求解;
(2)点B围绕点O逆时针旋转45°,落在y轴上,设为点B′(0,4),同理点C(0,﹣4![]() )围绕点O逆时针旋转45°,设旋转后该点对应点C′(4,﹣4),即可求解;
)围绕点O逆时针旋转45°,设旋转后该点对应点C′(4,﹣4),即可求解;
(3)在图2中,作直线y=﹣2x+4交抛物线于点N′,则抛物线和直线y=﹣2x+4绕原点O顺时针旋转45°得到新曲线和直线线y=3x﹣4![]() ,由ON=ON′,即可求解.
,由ON=ON′,即可求解.
解:(1)抛物线的表达式为:y=ax2+1,
将点A坐标代入上式得:2=a+1,解得:a=1,
故抛物线的表达式为:y=x2+1,
n=3×2![]() ﹣4
﹣4![]() =2
=2![]() ;
;
(2)∵点B的横坐标和纵坐标相同,BO=4,
故点B围绕点O逆时针旋转45°,落在y轴上,设为点B′(0,4),
同理点C(0,﹣4![]() )围绕点O逆时针旋转45°,设旋转后该点对应点C′(4,﹣4),
)围绕点O逆时针旋转45°,设旋转后该点对应点C′(4,﹣4),
将BC坐标代入一次函数表达式:y=mx+n得:![]() ,解得:
,解得:![]() ,
,
故旋转后直线的表达式为:y=﹣2x+4;
(3)在图2中,作直线y=﹣2x+4交抛物线于点N′,
则抛物线和直线y=﹣2x+4绕原点O顺时针旋转45°得到新曲线和直线线y=3x﹣4![]() ,
,
联立y=x2+1与y=﹣2x+4并解得:x=1或﹣3(舍去﹣3),故点N′(1,2),
设点N(m,3m﹣4![]() ),
),
由题意得:ON=ON′,
即:![]() ,解得:m=
,解得:m=![]() (不合题意值已舍去),
(不合题意值已舍去),
故点N′(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
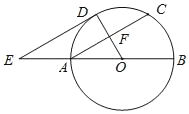
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接AD、CD、OC.填空
①当∠OAC的度数为 时,四边形AOCD为菱形;
②当OA=AE=2时,四边形ACDE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织学生参加“书法”、“摄影”、“航模”、“围棋”四个课外兴趣小组,要求每人必须参加,并且只能选择其中一个小组,为了解学生对四个课外兴趣小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的扇形统计图和条形统计图(部分信息未给出),请你根据给出的信息解答下列问题:

(1)求参加这次问卷调查的学生人数,并补全条形统计图(画图后请标注相应的数据);
(2)m=_______,n=_______;
(3)若该校共有1200名学生,试估计该校选择“围棋”课外兴趣小组的学生有多少人?
(4)分别用A、B、C、D表示“书法”、“摄影”、“航模”、“围棋”,小明和小红从中各选取一个小组,请用树状图法或列表法求出“两人选择小组不同”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家计划2035年前实施新能源汽车,某公司为加快新旧动能转换,提高公司经济效益,决定对近期研发出的一种新型能源产品进行降价促销.根据市场调查:这种新型能源产品销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个新型能源产品的成本为100元.
问:(1)设该产品的销售单价为![]() 元,每天的利润为
元,每天的利润为![]() 元.则
元.则![]() _________(用含
_________(用含![]() 的代数式表示)
的代数式表示)
(2)这种新型能源产品降价后的销售单价为多少元时,公司每天可获利32000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
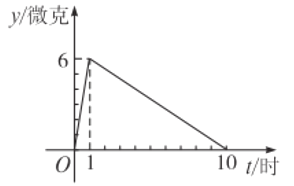
【题目】在抗击新型冠状病毒感染的肺炎疫情过程中,某医药研究所正在试研发一种抑制新型冠状病毒的药物,据临床观察:如果成人按规定的剂量注射这种药物,注射药物后每毫升血液中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间的关系近似地满足图中折线.
(小时)之间的关系近似地满足图中折线.
(1)求注射药物后每毫升血液中含药量![]() 与时间
与时间![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;
(2)据临床观察:每毫升血液中含药量不少于![]() 微克时,对控制病情是有效的.如果病人按规定的剂量注射 该药物后,求控制病情的有效时间.
微克时,对控制病情是有效的.如果病人按规定的剂量注射 该药物后,求控制病情的有效时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办园博会知识竞赛,打算购买A、B两种奖品.如果购买A奖品10件、B奖品5件,共需120元;如果购买A奖品5件、B奖品10件,共需90元.
(1)A,B两种奖品每件各多少元?
(2)若购买A、B奖品共100件,总费用不超过600元,则A奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,AD=2BC,点E为AD的中点,连接BE、BD,∠ABD=90°.

(1)如图l,求证:四边形BCDE为菱形;
(2)如图2,连接AC交BD于点F,连接EF,若AC平分∠BAD,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ABC面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形![]() 内接于⊙
内接于⊙![]() ,
,![]() 是⊙
是⊙![]() 的直径,过点
的直径,过点![]() 的切线与
的切线与![]() 的延长线相交于点
的延长线相交于点![]() .且
.且![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,当
,当![]() 时,求⊙
时,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com