
【题目】阅读探索题:
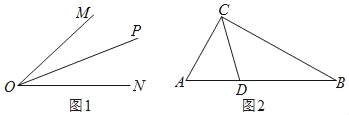
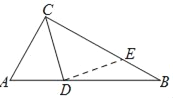
(1)如图1,OP是∠MON的平分线,以O为圆心任意长为半径作弧,分别交射线ON、OM于C、B两点,在射线OP上任取一点A(点O除外),连接AB、AC.求证:△AOB≌△AOC.
(2)请你参考以上方法,解答下列问题:
如图2,在 Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系并证明.
【答案】(1)证明见解析(2)证明见解析
【解析】
1)根据以O为圆心任意长为半径作弧,交射线ON,OM为C,B两点,OP是∠MON的平分线,运用SAS判定△AOB≌△AOC即可;
(2)先截取CE=CA,连接DE,根据SAS判定△CAD≌△CED,得出AD=DE,∠A=∠CED=60°,AC=CE,进而得出结论BC=AC+AD;
(1)
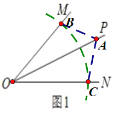
证明:在△AOB和△AOC中, 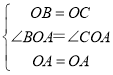
∴△AOB≌△AOC(SAS).
(2)
在CB上截取CE=CA,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
在△ACD和△ECD中, 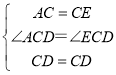
∴△ACD≌△ECD(SAS),
∴∠CAD=∠CED=60°,
∵∠ACB=90°,
∴∠B=30°,
∴∠EDB=30°,
即∠EDB=∠B,
∴DE=EB,
∵BC=CE+BE,
∴BC=AC+DE,
∴BC=AC+AD.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
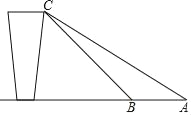
【题目】如图是东方货站传送货物的平面示意图,为了提高安全性,工人师傅打算减小传送带与地面的夹角,由原来的45°改为36°,已知原传送带BC长为4米,求新传送带AC的长及新、原传送带触地点之间AB的长.(结果精确到0.1米)参考数据:sin36°≈0.59,cos36°≈0.1,tan36°≈0.73,![]() 取1.414
取1.414
查看答案和解析>>
科目:初中数学 来源: 题型:
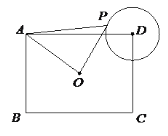
【题目】如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( )
A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市第一次用3000元购进某种干果销售,第二次又调拨9000元购进该种干果,但第二次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市先按每千克9元的价格出售,当大部分干果出售后,最后的600千克按原售价的7折售完,超市两次销售这种干果共盈利________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是AC的中点,点E在BC的延长线上,点F在AB上,![]() .若AB=5,则BE+BF的长度为( )
.若AB=5,则BE+BF的长度为( )
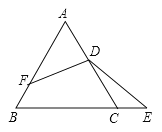
A.7.5B.8C.8.5D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(解决问题)如图1,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() .点
.点![]() 是
是![]() 边上任意一点,过点
边上任意一点,过点![]() 作
作![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() ,点
,点![]() .
.
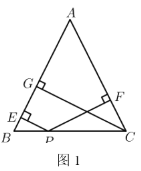
(1)若![]() ,
,![]() ,则
,则![]() 的面积是______,
的面积是______,![]() ______.
______.
(2)猜想线段![]() ,
,![]() ,
,![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
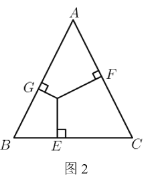
(3)(变式探究)如图2,在![]() 中,若
中,若![]() ,点
,点![]() 是
是![]() 内任意一点,且
内任意一点,且![]() ,
,![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() ,点
,点![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
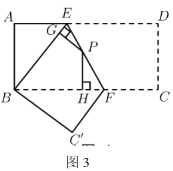
(4)(拓展延伸)如图3,将长方形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 上,点
上,点![]() 落在点
落在点![]() 处,点
处,点![]() 为折痕
为折痕![]() 上的任意一点,过点
上的任意一点,过点![]() 作
作![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() ,点
,点![]() .若
.若![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com