
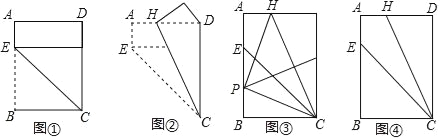
【题目】对给定的一张矩形纸片ABCD进行如下操作:先沿CE折叠,使点B落在CD边上(如图①),再沿CH折叠,这时发现点E恰好与点D重合(如图②)
(1)根据以上操作和发现,求![]() 的值;
的值;
(2)将该矩形纸片展开.
①如图③,折叠该矩形纸片,使点C与点H重合,折痕与AB相交于点P,再将该矩形纸片展开.求证:∠HPC=90°;
②不借助工具,利用图④探索一种新的折叠方法,找出与图③中位置相同的P点,要求只有一条折痕,且点P在折痕上,请简要说明折叠方法.(不需说明理由)
【答案】(1)![]() ;(2)①证明见解析;②见解析.
;(2)①证明见解析;②见解析.
【解析】(1)依据△BCE是等腰直角三角形,即可得到CE=![]() BC,由图②,可得CE=CD,而AD=BC,即可得到CD=
BC,由图②,可得CE=CD,而AD=BC,即可得到CD=![]() AD,即
AD,即![]() =
=![]() ;
;
(2)①由翻折可得,PH=PC,即PH2=PC2,依据勾股定理可得AH2+AP2=BP2+BC2,进而得出AP=BC,再根据PH=CP,∠A=∠B=90°,即可得到Rt△APH≌Rt△BCP(HL),进而得到∠CPH=90°;
②由AP=BC=AD,可得△ADP是等腰直角三角形,PD平分∠ADC,故沿着过D的直线翻折,使点A落在CD边上,此时折痕与AB的交点即为P;由∠BCE=∠PCH=45°,可得∠BCP=∠ECH,由∠DCE=∠PCH=45°,可得∠PCE=∠DCH,进而得到CP平分∠BCE,故沿着过点C的直线折叠,使点B落在CE上,此时,折痕与AB的交点即为P.
(1)由图①,可得∠BCE=![]() ∠BCD=45°,
∠BCD=45°,
又∵∠B=90°,
∴△BCE是等腰直角三角形,
∴![]() ,即CE=
,即CE=![]() BC,
BC,
由图②,可得CE=CD,而AD=BC,
∴CD=![]() AD,
AD,
∴![]() =
=![]() ;
;

(2)①设AD=BC=a,则AB=CD=![]() a,BE=a,
a,BE=a,
∴AE=(![]() ﹣1)a,
﹣1)a,
如图③,连接EH,则∠CEH=∠CDH=90°,
∵∠BEC=45°,∠A=90°,
∴∠AEH=45°=∠AHE,
∴AH=AE=(![]() ﹣1)a,
﹣1)a,
设AP=x,则BP=![]() a﹣x,由翻折可得,PH=PC,即PH2=PC2,
a﹣x,由翻折可得,PH=PC,即PH2=PC2,
∴AH2+AP2=BP2+BC2,
即[(![]() ﹣1)a]2+x2=(
﹣1)a]2+x2=(![]() a﹣x)2+a2,
a﹣x)2+a2,
解得x=a,即AP=BC,
又∵PH=CP,∠A=∠B=90°,
∴Rt△APH≌Rt△BCP(HL),
∴∠APH=∠BCP,
又∵Rt△BCP中,∠BCP+∠BPC=90°,
∴∠APH+∠BPC=90°,
∴∠CPH=90°;
②折法:如图,由AP=BC=AD,可得△ADP是等腰直角三角形,PD平分∠ADC,
故沿着过D的直线翻折,使点A落在CD边上,此时折痕与AB的交点即为P;
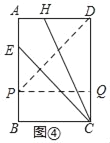
折法:如图,由∠BCE=∠PCH=45°,可得∠BCP=∠ECH,
由∠DCE=∠PCH=45°,可得∠PCE=∠DCH,
又∵∠DCH=∠ECH,
∴∠BCP=∠PCE,即CP平分∠BCE,
故沿着过点C的直线折叠,使点B落在CE上,此时,折痕与AB的交点即为P.



 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(a,0),(b,0),且满足![]() 现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.
现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)求点C,D的坐标及四边形ABDC的面积;
(2)在y轴上是否存在一点M,连接MA,MB,使S△MAB=S四边形ABDC?若存在这样一点,求出点M的坐标;若不存在,试说明理由;
(3)点P是射线BD上的一个动点(不与B,D重合),连接PC,PA,求∠CPA与∠DCP、∠BAP之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各图中的MA1与NAn平行.
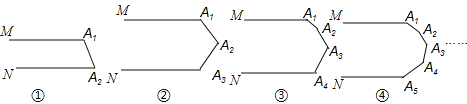
(1)图①中的∠A1+∠A2= 度,图②中的∠A1+∠A2+∠A3= 度,
图③中的∠A1+∠A2+∠A3+∠A4= 度,图④中的∠A1+∠A2+∠A3+∠A4+∠A5= 度,…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A10= 度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An= .
查看答案和解析>>
科目:初中数学 来源: 题型:
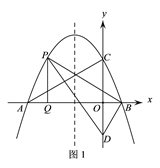
【题目】如图,抛物线y=-![]() x2-
x2-![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴于点C,已知点D(0,-
与x轴交于A、B两点(点A在点B的左侧),与y轴于点C,已知点D(0,-![]() ).
).
(1)求直线AC的解析式;
(2)如图1,P为直线AC上方抛物线上的一动点,当△PBD的面积最大时,过P作PQ⊥x轴于点Q,M为抛物线对称轴上的一动点,过M作y轴的垂线,垂足为点N,连接PM、NQ,求PM+MN+NQ的最小值;
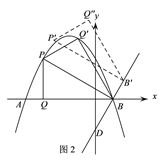
(3)在(2)问的条件下,将得到的△PBQ沿PB翻折得到△PBQ′,将△PBQ′沿直线BD平移,记平移中的△PBQ′为△P′B′Q″,在平移过程中,设直线P′B′与x轴交于点E,则是否存在这样的点E,使得△B′EQ″为等腰三角形?若存在,求此时OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.
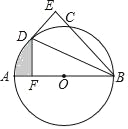
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,.过B作BE//AC.
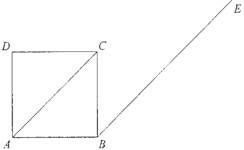
(1)求BE与AC之间的距离;
(2)F为BE上一点,连接AF,过C作CG//AF交BE于G.若∠FAB=15°,
①依题意补全图形;
②求证:四边形AFGC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(![]() )如图
)如图![]() ,
,![]() 中,
中,![]() ,
,![]() 是
是![]() 上任意一点,以点
上任意一点,以点![]() 为中心,取旋转角等于
为中心,取旋转角等于![]() ,把
,把![]() 逆时针旋转,画出旋转后的图形.
逆时针旋转,画出旋转后的图形.
(![]() )如图
)如图![]() ,等边
,等边![]() 中,
中,![]() 为
为![]() 边上一点,
边上一点,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
求证:![]() .
.
(![]() )已知:如图
)已知:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,已知
,已知![]() ,
,![]() .写出求线段
.写出求线段![]() 长的具体思路(即添加辅助线的方法,推导的具体步骤详写,其它的写出关键步骤或结果即可),并给出最后结果.
长的具体思路(即添加辅助线的方法,推导的具体步骤详写,其它的写出关键步骤或结果即可),并给出最后结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B,E,C,F在一条直线上,AC∥DE,∠A=∠D,AB=DF.
(1)试说明:△ABC≌△DFE;
(2)若BF=13,EC=7,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一条笔直的公路进行跑步训练,可以用如图所示一条直线上来刻画他在公路上跑步情境.假定向右跑步的路程记为正数,向左跑步的路程记为负数,则所跑步的各段路程依次记为:+5,-3,-6,+8,-6,+12,-10.(单位:百米)
(1)小明最后是否回到出发点![]() ?
?
(2)小明在跑步过程中距离出发点![]() 最远是多少米?.
最远是多少米?.
(3)在跑步过程中,如果小明每跑1千米会消耗约60卡热量,那么小明此次训练一共会消耗多少卡?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com