
 如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题.
如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题.分析 (1)由图象可求得A点的坐标,由解析式可求得抛物线的对称轴方程,利用图象的对称性可求得B点坐标;
(2)把B点坐标代入抛物线解析式可求得a的值;
(3)由抛物线解析式可求得P点坐标,再结合A、B坐标可求得AB的值,则可求得△PAB的面积.
解答 解:
(1)由图象可知A点坐标为(-3,0),
∵y=a(x+1)2+2,
∴抛物线对称轴方程为x=-1,
∵A、B两点关于对称轴对称,
∴B的坐标为(1,0),
故答案为:(-3,0);(1,0);
(2)将(1,0)代入y=a(x+1)2+2,
可得0=4a+2,解得a=-$\frac{1}{2}$;
(3)∵y=a(x+1)2+2,
∴抛物线的顶点坐标是(-1,2),
∵A(-3,0),B(1,0),
∴AB=XB-XA=1-(-3)=4,
∴S△PAB=$\frac{1}{2}$×4×2=4.
点评 本题主要考查二次函数的性质,掌握二次函数的对称轴及顶点坐标的求法是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{5}{3}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
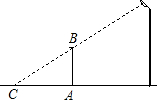 如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC﹙假定AC>AB﹚,影长的最大值为m,最小值为n,那么下列结论中:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.正确的结论序号是①③④.
如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC﹙假定AC>AB﹚,影长的最大值为m,最小值为n,那么下列结论中:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.正确的结论序号是①③④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是由两个长方体组成的几何体,这两个长方体的底面都是正方形,按要求完成下列各小题.
如图是由两个长方体组成的几何体,这两个长方体的底面都是正方形,按要求完成下列各小题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、B的坐标分别为(-1,-1),(-3,2).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、B的坐标分别为(-1,-1),(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A,F,E,B四点在同一直线上,AC⊥CE,BD⊥DF,AF=BE,AC=BD.试判断DF与CE的关系(指数量与位置关系),并说明理由.
如图,A,F,E,B四点在同一直线上,AC⊥CE,BD⊥DF,AF=BE,AC=BD.试判断DF与CE的关系(指数量与位置关系),并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,有一个圆柱,它的高为9厘米,底面周长为24厘米,在圆柱下底面的A点有一只蚂蚁要沿侧面到上底面B点取食物,问它爬行的最短路程是多少厘米?
如图所示,有一个圆柱,它的高为9厘米,底面周长为24厘米,在圆柱下底面的A点有一只蚂蚁要沿侧面到上底面B点取食物,问它爬行的最短路程是多少厘米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com