
【题目】在△ABC 中,∠ABC=60°,BC=8,点 D 是 BC 边的中点,点 E 是边 AC上一点,过点 D 作 ED 的垂线交边 AC 于点 F,若 AC=7CF,且 DE 恰好平分△ABC 的周长,则△ABC 的面积为______.

【答案】10
【解析】
取 AC 的中点 M,连接 DM,作 AH⊥BC 于 H.设 DM=a,AE=b.想办法证明 DM=EM=FM=a.AE=CF=b,2a=5b,解直角三角形求出 BH,CH 用 b 表示,根据边长的长构建方程求出 b 即可解决问题;
如图,取AC的中点M,连接DM,作AH⊥BC于H.
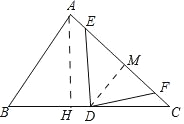
设 DM=a,AE=b.
∵BD=DC,AM=MC,
∴AB=2DM=2a,
∵AB+AE+BD=EC+DC,
∴EC=2a+b,AC=2a+2b,
∴AM=MC=a+b,
∴EM=a,
∴EM=DM,
∴∠MED=∠MDE,
∵∠MED+∠MFD=90°,∠MDE+∠MDF=90°,
∴∠MFD=∠MDF,
∴MD=MF=a,
∴CF=AE=b,
∵AC=7CF,
∴2a+2b=7b,
∴2a=5b,
∵AB=5b,AC=7b,
在 Rt△ABH 中,∵∠B=60°,
∴BH= ![]() AB=
AB= ![]() b,AH=
b,AH= ![]() b,
b,
在 Rt△ACH 中,CH=![]() =
=![]() b,
b,
∴BC=BH+HC=8b,
∴8b=8,
∴b=1,
∴S△ABC= ![]() ×8×
×8×![]() =10
=10![]() ,
,
故答案为: 10![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 面积为
面积为![]() ,延长
,延长![]() 至点
至点![]() ,使得
,使得![]() ,以
,以![]() 为边在正方形另一侧作菱形
为边在正方形另一侧作菱形![]() ,其中
,其中![]() ,依次延长
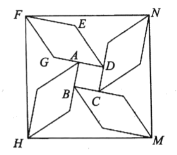
,依次延长![]() 类似以上操作再作三个形状大小都相同的菱形,形成风车状图形,依次连结点
类似以上操作再作三个形状大小都相同的菱形,形成风车状图形,依次连结点![]() 则四边形
则四边形![]() 的面积为___________.
的面积为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
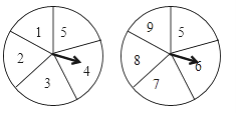
【题目】如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 ![]() :y=ax2 过点(2,2)
:y=ax2 过点(2,2)
(1)直接写出抛物线的解析式;
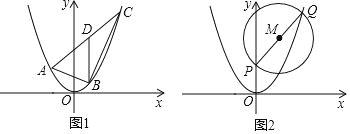
(2)如图,△ABC 的三个顶点都在抛物线![]() 上,且边 AC 所在的直线解析式为y=x+b,若 AC 边上的中线 BD 平行于 y 轴,求
上,且边 AC 所在的直线解析式为y=x+b,若 AC 边上的中线 BD 平行于 y 轴,求![]() 的值;
的值;
(3)如图,点 P 的坐标为(0,2),点 Q 为抛物线上![]() 上一动点,以 PQ 为直径作⊙M,直线 y=t 与⊙M 相交于 H、K 两点是否存在实数 t,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.
上一动点,以 PQ 为直径作⊙M,直线 y=t 与⊙M 相交于 H、K 两点是否存在实数 t,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块三角形空地上种草皮绿化,已知AB=20米,AC=30米,∠A=150°,草皮的售价为a元/米2,则购买草皮至少需要( )
A. 450a元 B. 225a元 C. 150a元 D. 300a元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)以O为中心作出△ABC的中心对称图形△A1B1C1,并写出点B1坐标;
(2)以格点P为旋转中心,将△ABC按顺时针方向旋转90°,得到△A′B′C′,且使点A的对应点A′的恰好落在△A1B1C1的内部格点上(不含△A1B1C1的边上),写出点P的坐标,并画出旋转后的△A′B′C′.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面关于x的方程中:①ax2+x+2=0;②3(x-9)2-(x+1)2=1;③x+3=![]() ④x2-a=0(a为任意实数
④x2-a=0(a为任意实数![]() ;⑤
;⑤![]() =x-1一元二次方程的个数是
=x-1一元二次方程的个数是![]()
![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com