
△ABC的各边长为3 cm,4 cm,5 cm.与其相似的另一个△A'B′C′的最大边为15 cm,那么它的周长为________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
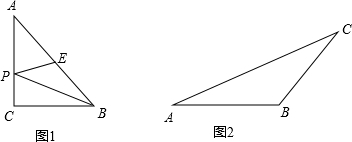
 某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决下列问题:
某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决下列问题:| x2+1 |
| (4-x)2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 10 |
| 10 |
| x2+1 |
| (4-x)2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| x2+1 |
| (4-x)2+4 |
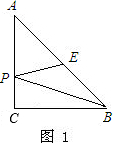
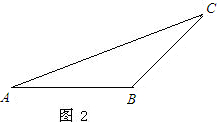
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com