
 如图,在?ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有( )
如图,在?ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 由翻折的性质可知,EB=EB',由E为AB的中点,得到EA=EB',根据三角形外角等于不相邻的两内角之和,找到与∠FEB相等的角,再根据AB∥CD,也可得到∠FEB=∠ACD.
解答 解:由翻折的性质可知:EB=EB',∠FEB=∠FEB';
∵E为AB的中点,
∴AE=BE=EB',
∴∠EAB=∠EBA,
∵∠BEB'=∠EAB+∠EB'A,
∴2∠FEB=2∠EAB=2∠EB'A,
∴∠FEB=∠EAB=∠EB'A,
∵AB∥CD,
∴∠BAE=∠ACD,
∴∠FEB=∠ACD,
∴与∠FEB相等的角有∠FEB',∠EAB,∠EB'A,∠ACD,
∴故选C.
点评 此题考查翻折的性质,EA=EB'是正确解答此题的关键


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
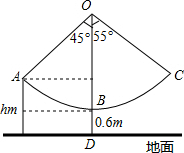 某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m)
某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
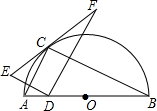 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com