
【题目】王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间x(单位:分钟)与学习收益量y的关系如图甲所示,用于回顾反思的时间x(单位:分钟)与学习收益量z的关系为z=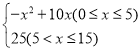 ,且用于回顾反思的时间不超过用于解题的时间.
,且用于回顾反思的时间不超过用于解题的时间.
(1)求王亮解题的学习收益量y与用于解题的时间x之间的函数关系式,并写出自变量x的取值范围;
(2)王亮如何分配解题和回顾反思的时间,才能使这30分钟的学习收益总量最大?(学习收益总量=解题的学习收益量+回顾反思的学习收益量)
【答案】(1)y=2x. 自变量x的取值范围是:15≤x≤30;(2)解题的时间为26分钟,用于回顾反思的时间为4分钟时,学习收益总量最大.
【解析】
(1)设王亮解题的学习收益量y与用于解题的时间x之间的函数关系式为y=kx,观察图象可知该函数图象过点(2,4),代入即可求得k值,由此即可求得函数解析式,根据题意直接确定x的取值范围即可;(2)设王亮用于回顾反思的时间为x(0≤x≤15)分钟,学习效益总量为W,分当0≤x≤5时和当5<x≤15时两种情况求得w与x的函数关系式,根据函数的性质求得w的最大值,比较即可解答.
解:(1)设y=kx,把(2,4)代入,
得:k=2,
∴y=2x.
自变量x的取值范围是:15≤x≤30.
(2)设王亮用于回顾反思的时间为x(0≤x≤15)分钟,学习效益总量为W,
则他用于解题的时间为(30﹣x)分钟.
当0≤x≤5时,W=﹣x2+10x+2(30﹣x)=﹣x2+8x+60=﹣(x﹣4)2+76.
∴当x=4时,W最大=76.
当5<x≤15时,W=25+2(30﹣x)=﹣2x+85.
∵W随x的增大而减小,
∴当x=5时,W最大=75
综合所述,当x=4时,W最大=76,此时30﹣x=26.
即王亮用于解题的时间为26分钟,用于回顾反思的时间为4分钟时,学习收益总量最大.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】问题提出:
如图,图①是一张由三个边长为 1 的小正方形组成的“L”形纸片,图②是一张 a× b 的方格纸(a× b的方格纸指边长分别为 a,b 的矩形,被分成 a× b个边长为 1 的小正方形,其中 a≥2 , b≥2,且 a,b 为正整数) .把图①放置在图②中,使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?
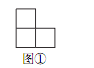
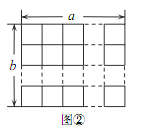
问题探究:
为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论.
探究一:
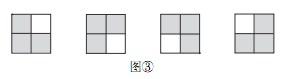
把图①放置在 2× 2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图③,对于 2×2的方格纸,要用图①盖住其中的三个小正方形,显然有 4 种不同的放置方法.
探究二:
把图①放置在 3×2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图④,在 3×2的方格纸中,共可以找到 2 个位置不同的 2 ×2方格,依据探究一的结论可知,把图①放置在 3×2 的方格纸中,使它恰好盖住其中的三个小正方形,共有 2 ×4=8种
不同的放置方法.
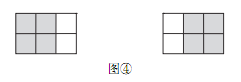
探究三:
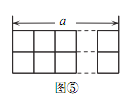
把图①放置在 a ×2 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图⑤, 在 a ×2 的方格纸中,共可以找到______个位置不同的 2×2方格,依据探究一的结论可知,把图①放置在 a× 2 的方格纸中,使它恰好盖住其中的三个小正方形,共有______种不同的放置方法.
探究四:
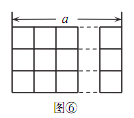
把图①放置在 a ×3 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图⑥,在 a ×3 的方格纸中,共可以找到______个位置不同的 2×2方格,依据探究一的结论可知,把图①放置在 a ×3 的方格纸中,使它恰好盖住其中的三个小正方形,共有_____种不同的放置方法.
……
问题解决:
把图①放置在 a ×b的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?(仿照前面的探究方法,写出解答过程,不需画图.)
问题拓展:
如图,图⑦是一个由 4 个棱长为 1 的小立方体构成的几何体,图⑧是一个长、宽、高分别为 a,b ,c (a≥2 , b≥2 , c≥2 ,且 a,b,c 是正整数)的长方体,被分成了a×b×c个棱长为 1 的小立方体.在图⑧的不同位置共可以找到______个图⑦这样的几何体.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() x+6与x、y轴分别交于点A,点B,双曲线的解析式为
x+6与x、y轴分别交于点A,点B,双曲线的解析式为![]()

(1)求出线段AB的长
(2)在双曲线第四象限的分支上存在一点C,使得CB⊥AB,且CB=AB,求k的值;
(3)在(1)(2)的条件下,连接AC,点D为BC的中点,过D作AC的垂线BF,交AC于B,交直线AB于F,连AD,若点P为射线AD上的一动点,连接PC、PF,当点P在射线AD上运动时,PF![]() -PC
-PC![]() 的值是否发生改变?若改变,请求出其范围;若不变,请证明并求出定值。
的值是否发生改变?若改变,请求出其范围;若不变,请证明并求出定值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=60°,AD=4,点F是AB的中点,过点F作FE⊥AD,垂足为E,将△AEF沿点A到点B的方向平移,得到△A'E'F',设点P、P'分别是EF、E'F'的中点,当点A'与点B重合时,四边形PP'CD的面积为( )
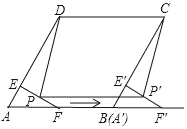
A. 7![]() B. 6
B. 6![]() C. 8
C. 8![]() D. 8
D. 8![]() ﹣4
﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长18千米的乡村公路,已知甲工程队比乙工程队每天多修路0.6千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.6万元,乙工程队每天的修路费用为0.5万元,要使两个工程队修路总费用不超过6.3万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
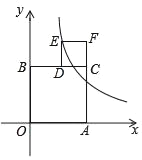
【题目】如图,四边形AOBC和四边形CDEF都是正方形,边OA在x轴上,边OB在y轴上,点D在边CB上,反比例函数![]() (k>0)在第一象限的图象经过点E,若正方形AOBC和正方形CDEF的面积之差为6,则k=_____.
(k>0)在第一象限的图象经过点E,若正方形AOBC和正方形CDEF的面积之差为6,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,抛物线y=ax2+bx+c经过点A(﹣2,0)、B(4,0)、C(0,3)三点.
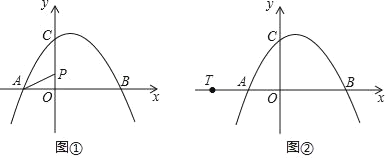
(1)试求抛物线的解析式;
(2)点P是y轴上的一个动点,连接PA,试求5PA+4PC的最小值;
(3)如图②,若直线l经过点T(﹣4,0),Q为直线l上的动点,当以A、B、Q为顶点所作的直角三角形有且仅有三个时,试求直线l的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AB=AC,E是边BC上的点,且∠AED=∠CAD,DE交AC于点F.
(1)求证:△ABE∽△DAF;
(2)当ACFC=AEEC时,求证:AD=BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
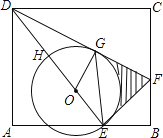
【题目】如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F
(1)求证:△ADE∽△BEF;
(2)设H是ED上一点,以EH为直径作⊙O,DF与⊙O相切于点G,若DH=OH=3,求图中阴影部分的面积(结果保留到小数点后面第一位,![]() ≈1.73,π≈3.14).
≈1.73,π≈3.14).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com