
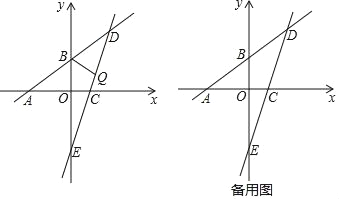
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬Ņ»“ĪŗÆŹż![]() µÄĶ¼Ļó·Ö±šÓėxÖį”¢yÖįĻą½»ÓŚµćA”¢B£¬ĒŅÓė¾¹żµćC£Ø2£¬0£©µÄŅ»“ĪŗÆŹży=kx+bµÄĶ¼ĻóĻą½»ÓŚµćD£¬µćDµÄŗį×ų±źĪŖ4£¬Ö±ĻßCDÓėyÖįĻą½»ÓŚµćE£®
µÄĶ¼Ļó·Ö±šÓėxÖį”¢yÖįĻą½»ÓŚµćA”¢B£¬ĒŅÓė¾¹żµćC£Ø2£¬0£©µÄŅ»“ĪŗÆŹży=kx+bµÄĶ¼ĻóĻą½»ÓŚµćD£¬µćDµÄŗį×ų±źĪŖ4£¬Ö±ĻßCDÓėyÖįĻą½»ÓŚµćE£®
£Ø1£©Ö±ĻßCDµÄŗÆŹż±ķ“ļŹ½ĪŖ”” ””£»£ØÖ±½ÓŠ“³ö½į¹ū£©
£Ø2£©µćQĪŖĻ߶ĪDEÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓBQ£®
¢ŁČōÖ±ĻßBQ½«”÷BDEµÄĆ껿·ÖĪŖ1£ŗ2Į½²æ·Ö£¬ŹŌĒóµćQµÄ×ų±ź£»
¢Ś½«”÷BQDŃŲ×ÅÖ±ĻßBQ·ÕŪ£¬Ź¹µĆµćDĒ”ŗĆĀäŌŚÖ±ĻßABĻĀ·½µÄ×ų±źÖįÉĻ,ĒėÖ±½ÓŠ“³öµćQµÄ×ų±ź: .
”¾“š°ø”æ£Ø1£©y=3x©6£»£Ø2£©¢Ł£Ø![]() £¬©2£©»ņ£Ø
£¬©2£©»ņ£Ø![]() £¬2£©£»¢Ś“ęŌŚ£¬µćQµÄ×ų±źĪŖ£Ø3£¬3£©»ņ£Ø
£¬2£©£»¢Ś“ęŌŚ£¬µćQµÄ×ų±źĪŖ£Ø3£¬3£©»ņ£Ø![]() £¬
£¬![]() £©£®
£©£®
”¾½āĪö”æ
£Ø1£©Ēó³öC”¢DĮ½µć×ų±ź¼“æɽā¾öĪŹĢā£»
£Ø2£©¢Ł·ÖĮ½ÖÖĒéŠĪS”÷BEQ=![]() S”÷BDE»ņS”÷BEQ=
S”÷BDE»ņS”÷BEQ=![]() S”÷BDE·Ö±š¹¹½Ø·½³Ģ¼“æÉ£»
S”÷BDE·Ö±š¹¹½Ø·½³Ģ¼“æÉ£»
¢Ś·ÖĮ½ÖÖĒéŠĪ£ŗµ±µćDĀäŌŚxÕż°ėÖįÉĻ£Ø¼ĒĪŖµćD1£©Ź±£¬ČēĶ¼2ÖŠ£»µ±µćDĀäŌŚyøŗ°ėÖįÉĻ£Ø¼ĒĪŖµćD2£©Ź±£¬ČēĶ¼3ÖŠ£»·Ö±šĒó½ā¼“æÉ.
½ā£ŗ£Ø1£©ÓÉĢāŅā£ŗD£Ø4£¬6£©£¬C£Ø2£¬0£©£¬
ÉčÖ±ĻßCDµÄ½āĪöŹ½ĪŖy=kx+b£¬
ŌņÓŠ![]() £¬
£¬
½āµĆ![]() £¬
£¬
”ąÖ±ĻßCDµÄ½āĪöŹ½ĪŖy=3x©6£¬
¹Ź“š°øĪŖ£ŗy=3x©6£»
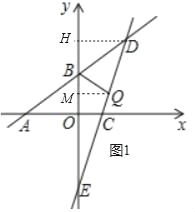
£Ø2£©¢Ł”ßÖ±ĻßBQ½«”÷BDEµÄĆ껿·ÖĪŖ1£ŗ2Į½²æ·Ö£¬
”ąS”÷BEQ=![]() S”÷BDE»ņS”÷BEQ=
S”÷BDE»ņS”÷BEQ=![]() S”÷BDE£¬
S”÷BDE£¬
ŌŚy=![]() x+3ÖŠ£¬µ±x=0Ź±£¬y=3£»µ±x=4Ź±£¬y=6£¬
x+3ÖŠ£¬µ±x=0Ź±£¬y=3£»µ±x=4Ź±£¬y=6£¬
”ąB£Ø0£¬3£©£¬D£Ø4£¬6£©£®
ŌŚy=3x©6ÖŠ£¬µ±x=0Ź±£¬y=©6£¬
”ąE£Ø0£¬©6£©£¬
”ąBE=9£¬
ČēĶ¼1ÖŠ£¬¹żµćD×÷DH”ĶyÖįÓŚµćH£¬ŌņDH=4£¬
”ąS”÷BDE=![]() BEDH=
BEDH=![]() ”Į9”Į4=18£¬
”Į9”Į4=18£¬
”ąS”÷BEQ=![]() ”Į18=6»ņS”÷BEQ=
”Į18=6»ņS”÷BEQ=![]() ”Į18=12£¬
”Į18=12£¬
ÉčQ£Øt£¬3t©6£©£¬ÓÉĢāŅāÖŖt£¾0£¬
¹żµćQ×÷QM”ĶyÖįÓŚµćM£¬ŌņQM=t£¬
”ą![]() ”Į9”Įt=12£¬
”Į9”Įt=12£¬
½āµĆt=![]() »ņ
»ņ![]() £¬
£¬
µ±t=![]() Ź±£¬3t©6=©2£¬
Ź±£¬3t©6=©2£¬
µ±t=![]() Ź±3t©6=2£¬
Ź±3t©6=2£¬
”ąQµÄ×ų±źĪŖ£Ø![]() £¬©2£©»ņ£Ø
£¬©2£©»ņ£Ø![]() £¬2£©£»
£¬2£©£»
¢Śµ±µćDĀäŌŚxÕż°ėÖįÉĻ£Ø¼ĒĪŖµćD1£©Ź±£¬ČēĶ¼2ÖŠ£¬
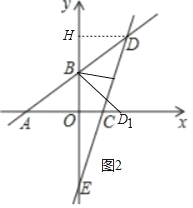
ÓÉ£Ø2£©ÖŖB£Ø0£¬3£©£¬D£Ø4£¬6£©£¬
”ąBH=BO=3£¬
ÓÉ·ÕŪµĆBD=BD1£¬
ŌŚ”÷Rt”÷DHBŗĶRt”÷D1OBÖŠ£¬
![]() £¬
£¬
”ąRt”÷DHB”ÕRt”÷D1OB£ØHL£©£¬
”ą”ĻDBH=”ĻD1BO£¬
ÓÉ·ÕŪµĆ”ĻDBQ=”ĻD1BQ£¬
”ą”ĻHBQ=”ĻOBQ=90”ć£¬
”ąBQ”ĪxÖį£¬
”ąµćQµÄׯ×ų±źĪŖ3£¬
ŌŚy=3x©6ÖŠ£¬µ±y=3Ź±£¬x=3£¬
”ąQ£Ø3£¬3£©£»
µ±µćDĀäŌŚyøŗ°ėÖįÉĻ£Ø¼ĒĪŖµćD2£©Ź±£¬ČēĶ¼3ÖŠ£¬
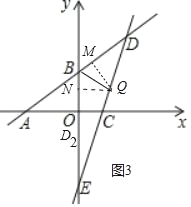
¹żµćQ×÷QM”ĶBD£¬QN”ĶOB£¬“¹×ć·Ö±šĪŖµćM”¢N£¬
ÓÉ·ÕŪµĆ”ĻDBQ=”ĻD2BQ£¬
”ąQM=QN£¬
ÓÉ£Ø2£©ÖŖS”÷BDE=18£¬¼“S”÷BQD+S”÷BQE=18£¬
”ą![]() BDQM+
BDQM+![]() BEQN=18£¬
BEQN=18£¬
ÓÉĮ½µćÖ®¼äµÄ¾ąĄė¹«Ź½£¬µĆBD=![]() =5£¬
=5£¬
”ą![]() ”Į5QN+
”Į5QN+![]() ”Į9QN=18£¬
”Į9QN=18£¬
½āµĆQN=![]() £¬
£¬
”ąµćQµÄŗį×ų±źĪŖ![]() £¬
£¬
ŌŚy=3x©6ÖŠ£¬µ±x=![]() Ź±£¬y=
Ź±£¬y=![]() £¬
£¬
”ąQ£Ø![]() £¬
£¬![]() £©£®
£©£®
×ŪŗĻÖŖ£¬µćQµÄ×ų±źĪŖ£Ø3£¬3£©»ņ£Ø![]() £¬
£¬![]() £©£®
£©£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻBACŗĶ”ĻABCµÄĘ½·ÖĻßĻą½»ÓŚµćO£¬¹żµćO×÷EF”ĪAB½»BCÓŚF£¬½»ACÓŚE£¬¹żµćO×÷OD”ĶBCÓŚD£¬ĻĀĮŠĖÄøö½įĀŪ£ŗ
¢Ł”ĻAOB=90”ć+![]() ”ĻC£»¢ŚAE+BF=EF£»¢Ūµ±”ĻC=90”揱£¬E£¬F·Ö±šŹĒAC£¬BCµÄÖŠµć£»¢ÜČōOD=a£¬CE+CF=2b£¬ŌņS”÷CEF=ab£®ĘäÖŠÕżČ·µÄŹĒ£Ø””””£©
”ĻC£»¢ŚAE+BF=EF£»¢Ūµ±”ĻC=90”揱£¬E£¬F·Ö±šŹĒAC£¬BCµÄÖŠµć£»¢ÜČōOD=a£¬CE+CF=2b£¬ŌņS”÷CEF=ab£®ĘäÖŠÕżČ·µÄŹĒ£Ø””””£©

A. ¢Ł¢Ś B. ¢Ū¢Ü C. ¢Ł¢Ś¢Ü D. ¢Ł¢Ū¢Ü
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ£ŗ”ĻMON=30”ć£¬µćA1”¢A2”¢A3ŌŚÉäĻßONÉĻ£¬µćB1”¢B2”¢B3”ŌŚÉäĻßOMÉĻ£¬”÷A1B1A2”¢”÷A2B2A3”¢”÷A3B3A4”¾łĪŖµČ±ßČż½ĒŠĪ£¬ČōOA1=1£¬Ōņ”÷A6B6A7µÄ±ß³¤ĪŖ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
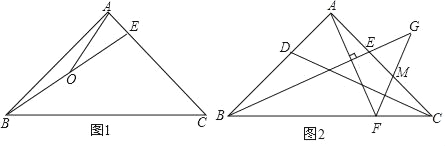
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬ŅŃÖŖAB=AC£¬”ĻBAC=90”ć£¬EĪŖ±ßACÉĻŅ»µć£¬Į¬½ÓBE£®
(1)ČēĶ¼1£¬Čō”ĻABE=15”ć£¬OĪŖBEÖŠµć£¬Į¬½ÓAO£¬ĒŅAO=1£¬ĒóBCµÄ³¤£»
(2)ČēĶ¼2£¬DĪŖABÉĻŅ»µć£¬ĒŅĀś×ćAE=AD£¬¹żµćA×÷AF”ĶBE½»BCÓŚµćF£¬¹żµćF×÷FG”ĶCD½»BEµÄŃÓ³¤ĻßÓŚµćG£¬½»ACÓŚµćM£¬ĒóÖ¤£ŗBG=AF+FG£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚÉżĘģ½įŹųŗ󣬊”ĆśĻėĄūÓĆĖłŃ§ŹżŃ§ÖŖŹ¶²āĮæѧŠ£ĘģøĖøß¶Č£¬ČēĶ¼£¬ĘģøĖµÄ¶„¶Ė“¹ĻĀŅ»Éž×Ó£¬½«Éž×ÓĄÖ±¶¤ŌŚµŲÉĻ£¬Ä©¶ĖĒ”ŗĆÖĮC“¦ĒŅÓėµŲĆę³É60”ć½Ē£¬Š”Ćś“ÓÉž×ÓÄ©¶ĖC“¦ÄĆʚɞ×ÓŗóĶĖÖĮEµć£¬ĒóĘģøĖABµÄø߶ČŗĶŠ”ĆśŗóĶĖµÄ¾ąĄė£®£Øµ„Ī»£ŗĆ×£¬²Īæ¼Źż¾Ż£ŗ![]() ”Ö1.41£¬
”Ö1.41£¬![]() ”Ö1.73£¬½į¹ū±£ĮōŅ»Ī»Š”Źż£©
”Ö1.73£¬½į¹ū±£ĮōŅ»Ī»Š”Źż£©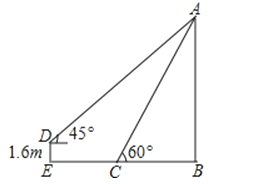
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŌO£Ø0£¬0£©”¢A£Ø2£¬0£©ĪŖ¶„µć×÷Õż”÷OAP1 £¬ ŅŌµćP1ŗĶĻ߶ĪP1AµÄÖŠµćBĪŖ¶„µć×÷Õż”÷P1BP2 £¬ ŌŁŅŌµćP2ŗĶĻ߶ĪP2BµÄÖŠµćCĪŖ¶„µć×÷”÷P2CP3 £¬ ”£¬Čē“Ė¼ĢŠųĻĀČ„£¬ŌņµŚĮłøöÕżČż½ĒŠĪÖŠ£¬²»ŌŚµŚĪåøöÕżČż½ĒŠĪÉĻµÄ¶„µćP6µÄ×ų±źŹĒ £® 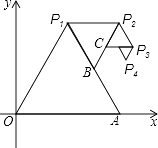
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹży=kx+b£Øk”Ł0£©µÄĶ¼Ļó¹żµćP£Ø© ![]() £¬0£©£¬ĒŅÓė·“±ČĄżŗÆŹży=
£¬0£©£¬ĒŅÓė·“±ČĄżŗÆŹży= ![]() £Øm”Ł0£©µÄĶ¼ĻóĻą½»ÓŚµćA£Ø©2£¬1£©ŗĶµćB£®
£Øm”Ł0£©µÄĶ¼ĻóĻą½»ÓŚµćA£Ø©2£¬1£©ŗĶµćB£® 
£Ø1£©ĒóŅ»“ĪŗÆŹżŗĶ·“±ČĄżŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ĒóµćBµÄ×ų±ź£¬²¢øł¾ŻĶ¼Ļó»Ų“š£ŗµ±xŌŚŹ²Ć“·¶Ī§ÄŚČ”ÖµŹ±£¬Ņ»“ĪŗÆŹżµÄŗÆŹżÖµŠ”ÓŚ·“±ČĄżŗÆŹżµÄŗÆŹżÖµ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
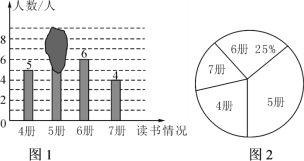
”¾ĢāÄæ”æĄĻŹ¦Ė껜³é²éĮĖ±¾Ń§ĘŚŃ§Éś¶ĮæĪĶāŹé²įŹżµÄĒéæö£¬»ęÖĘ³ÉĢõŠĪĶ³¼ĘĶ¼(ČēĶ¼1)ŗĶ²»ĶźÕūµÄÉČŠĪĶ¼(ČēĶ¼2)£¬ĘäÖŠĢõŠĪĶ³¼ĘĶ¼±»Ä«¼£ÕŚøĒĮĖŅ»²æ·Ö£®
(1)ĒóĢõŠĪĶ³¼ĘĶ¼ÖŠ±»ÕŚøĒµÄŹż£¬²¢Š“³ö²įŹżµÄÖŠĪ»Źż£»
(2)ĖęŗóÓÖ²¹²éĮĖĮķĶā¼øČĖ£¬µĆÖŖ×īÉŁµÄ¶ĮĮĖ6²į£¬½«ĘäÓėÖ®Ē°µÄŹż¾ŻŗĻ²¢ŗ󣬷¢ĻÖ²įŹżµÄÖŠĪ»ŹżĆ»ÓŠøı䣬Ōņ×ī¶ą²¹²éĮĖ____ČĖ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
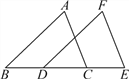
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCŃŲÖ±ĻßlĻņÓŅŅĘĮĖ3ĄåĆ×£¬µĆ”÷FDE£¬ĒŅBC£½6ĄåĆ×£¬”ĻB£½40”ć.
(1)ĒóBE£»
(2)Ēó”ĻFDBµÄ¶ČŹż£»
(3)ÕŅ³öĶ¼ÖŠĻąµČµÄĻ߶Ī(²»ĮķĢķ¼ÓĻ߶Ī)£»
(4)ÕŅ³öĶ¼ÖŠ»„ĻąĘ½ŠŠµÄĻ߶Ī(²»ĮķĢķ¼ÓĻ߶Ī)£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com