
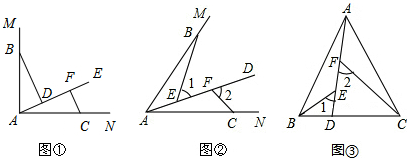
���� ����֤��������AAS֤����ABD�ա�CAF��
���̽��������AAS֤�����ɣ�
��չӦ�ã��������̽���Ľ��ۡ������ε������ʽ���㼴�ɣ�
��� ����֤����
֤������CF��AE��BD��AE��
���ADB=��CFA=90�㣬
�ߡ�MAN=90�㣬
���ABD+��BAD=90�㣬�֡�CAF+��BAD=90�㣬
���ABD=��CAF��
�ڡ�ABD�͡�CAF�У�
$\left\{\begin{array}{l}{��ABD=��CAF}\\{��ADB=��CFA}\\{AB=AC}\end{array}\right.$��
���ABD�ա�CAF��
���̽����
֤�����ߡ�1=��2��
���ABE=��CAF��
�ߡ�1=��ABE+��EAB����1=��BAC��
���ABE=��CAF��
�ڡ�ABE�͡�CAF�У�
$\left\{\begin{array}{l}{��AEB=��CFA}\\{��ABE=��CAF}\\{AB=AC}\end{array}\right.$��
���ABE�ա�CAF��
��չӦ�ã��ߡ�ABC�����Ϊ15��CD=2BD��
���ABD�����Ϊ15��$\frac{1}{3}$=5��
�����̽���ã���ABE�ա�CAF��
���ACF���BDE�����֮��=��ABD�����=5��
�ʴ�Ϊ��5��
���� ���⿼�����������ȫ�ȵ��ж������ʣ�����ȫ�������ε����ʶ������ж������ǽ���Ĺؼ���


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д� ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
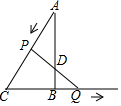 ��ͼ���ڡ�ABC�С�ABC=90�㣬��A=30�㣬BC=2cm������P��3cm/s���ٶ���A������AC�����˶�������Qͬʱ��1cm/s���ٶ���B��CB���ӳ��߷����˶�����PQ��ֱ��AB��D�����˶�ʱ��Ϊ$\frac{1}{2}$��3��$\frac{5\sqrt{3}+3}{11}$sʱ����ADP�ǵ��������Σ�
��ͼ���ڡ�ABC�С�ABC=90�㣬��A=30�㣬BC=2cm������P��3cm/s���ٶ���A������AC�����˶�������Qͬʱ��1cm/s���ٶ���B��CB���ӳ��߷����˶�����PQ��ֱ��AB��D�����˶�ʱ��Ϊ$\frac{1}{2}$��3��$\frac{5\sqrt{3}+3}{11}$sʱ����ADP�ǵ��������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a��b�� | B�� | ��a��-b�� | C�� | ��-a��b�� | D�� | ��-a��-b�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | 2 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������� | B�� | �۽������� | C�� | �ȱ������� | D�� | ����ֱ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ֻ��һ��ʵ���� | B�� | ��������ȵ�ʵ���� | ||
| C�� | ����������ȵ�ʵ���� | D�� | û��ʵ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a=$\sqrt{{a}^{2}}$=��$\sqrt{a}$��2 | B�� | ��$\sqrt{{a}^{2}}$=a����a=��$\sqrt{a}$��2 | C�� | ��2$\sqrt{-7}$��2=28 | D�� | 2$\sqrt{��-4��^{2}}$=-8 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com