
【题目】如图,线段AB , AD交于点A . C为直线AD上一点(不与点A , D重合).过点C在BC的右侧作射线CE⊥BC , 过点D作直线DF∥AB , 交CE于点G(G与D不重合).
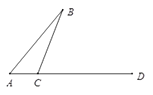
(1)如图1,若点C在线段AD上,且∠BCA为钝角.①按要求补全图形;②判断∠B与∠CGD的数量关系,并证明.
(2)若点C在线段DA的延长线上,请直接写出∠B与∠CGD的数量关系;
(3)请你结合本题的题意提出一个新的拓展问题 .
【答案】
(1)
解:①补全图形如图

②判断:∠CGD-∠B=90°.
证明 :过点C作CH∥AB,
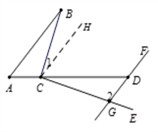
∴ ∠1=∠B(两直线平行,内错角相等).
∵ AB∥DF(已知),
∴ CH∥DF(平行于同一直线的两直线平行).
∴ ∠2+∠HCG=180°(两直线平行,同旁内角互补) .
∵ CE⊥BC(已知),
∴ ∠1+∠HCG=90°(垂直的定义).
∴ ∠CGD-∠B=90°
(2)∠CGD+∠B=90°
(3)若点C在线段AD的延长线上,∠B与∠CGD的数量关系是否会发生变化?![]() 若点C在线段AD的延长线上,∠B与∠CGD的数量关系是否会发生变化?
若点C在线段AD的延长线上,∠B与∠CGD的数量关系是否会发生变化?![]() 若点C在线段AD上,且∠BCA为锐角时,(1)中的结论还成立吗?
若点C在线段AD上,且∠BCA为锐角时,(1)中的结论还成立吗?
【解析】(1)①补全图形见解析;②先作辅助线,由∠2+∠HCG=180°和∠1+∠HCG=90°,推出结论∠CGD-∠B=90°即可;
(2)由(1)中②的结论可推导出结论∠CGD+∠B=90°. 附加题见解析.
(3)1.若点C在线段AD的延长线上,∠B与∠CGD的数量关系是否会发生变化?
2.若点C在线段AD上,且∠BCA为锐角时,(1)中的结论还成立吗?
【考点精析】本题主要考查了垂线的性质和平行线的判定与性质的相关知识点,需要掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
【题目】(2016·赤峰)为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查.如图,一测量船在A岛测得B岛在北偏西30°方向,C岛在北偏东15°方向,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离.(结果保留到整数, ![]() ≈1.41,
≈1.41, ![]() ≈2.45)
≈2.45)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成如下不完整的统计表与统计图:
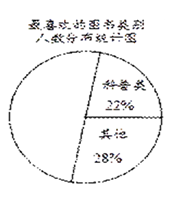

请结合图中的信息解答下列问题:
(1)随机抽取的样本容量a为;
(2)补全扇形统计图和条形统计图;
(3)已知该校有600名学生,估计全校最喜欢文学类图书的学生有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区注重城市绿化提高市民生活质量,新建林荫公园计划购买甲、乙两种树苗共800株,甲种树苗每株12元,乙种树苗每株15元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.
(1)若购买这两种树苗共用去10500元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个布袋中装有红、白两种颜色的小球,它们除颜色外没有任何其他区别.其中红球若干,白球5个,袋中的球已搅匀.若从袋中随机取出1个球,取出红球的可能性大,则红球的个数是( )
A. 4个B. 5个C. 不足4个D. 6个或6个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水龙头关闭不严会造成滴水,容器内盛水量w(L)与滴水时间t(h)的关系用可以显示水量的容器做如图1的试验,并根据试验数据绘制出如图2的函数图象,结合图象解答下列问题. 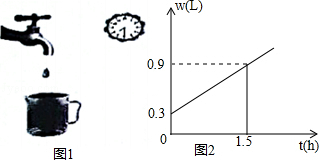
(1)容器内原有水多少升?
(2)求w与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com