
 如图,已知动点A在反比例函数y=$\frac{2}{x}$(x>0)图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA到点D,使AD=$\frac{1}{2}$AB,延长BA到点E,使AE=$\frac{1}{2}$AC,直线DE分别交x、y轴于点P、Q,当$\frac{QE}{DP}$=$\frac{4}{9}$时,则△ACE与△ADB面积之和等于$\frac{13}{12}$.
如图,已知动点A在反比例函数y=$\frac{2}{x}$(x>0)图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA到点D,使AD=$\frac{1}{2}$AB,延长BA到点E,使AE=$\frac{1}{2}$AC,直线DE分别交x、y轴于点P、Q,当$\frac{QE}{DP}$=$\frac{4}{9}$时,则△ACE与△ADB面积之和等于$\frac{13}{12}$. 分析 作DF⊥x轴于点F,EG⊥y轴于G,得到△QEG∽△PDF,于是得到$\frac{EG}{PF}$=$\frac{QE}{DP}$=$\frac{4}{9}$,设EG=4t,则PF=9t,然后根据△ADE∽△FPD,据此即可得到关于t的方程,求得t的值,进而求解.
解答 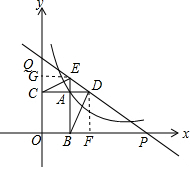 解:作DF⊥x轴于点F,EG⊥y轴于G,
解:作DF⊥x轴于点F,EG⊥y轴于G,
∴△QEG∽△DPF,
∴$\frac{EG}{PF}$=$\frac{QE}{DP}$=$\frac{4}{9}$,
设EG=4t,则PF=9t,
∴A(4t,$\frac{1}{2t}$),
∵AE=$\frac{1}{2}$AC,AD=$\frac{1}{2}$AB,
∴AE=2t,AD=$\frac{1}{4t}$,DF=$\frac{1}{2t}$,PF=9t,
∵△ADE∽△FPD,
∴AE:DF=AD:PF,即2t:$\frac{1}{2t}$=$\frac{1}{4t}$:9t,即t2=$\frac{1}{12}$,
△ACE与△ADB面积之和=$\frac{1}{2}$×2t×4t+$\frac{1}{2}$×$\frac{1}{4t}$×$\frac{1}{2t}$=$\frac{13}{12}$.
故答案为:$\frac{13}{12}$.
点评 本题考查了反比例函数综合题,涉及到从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|,也考查了相似三角形的判定与性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 射击总次数n | 10 | 20 | 50 | 100 | 200 | 500 | 1000 |
| 击中靶心次数m | 9 | 16 | 41 | 88 | 168 | 429 | 861 |
| 击中靶心频率 $\frac{m}{n}$ | 0.9 | 0.8 | 0.82 | 0.88 | 0.84 | 0.858 | 0.861 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1=y3<y2 | B. | y1>y2>y3 | C. | y1>y3<y2 | D. | y2>y1>y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售单价x元/公斤 | … | 30 | 35 | 40 | 45 | … |
| 销售量y公斤 | … | 500 | 450 | 400 | 350 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 190×lO8 | B. | 1.9×1010 | C. | 0.19×1011 | D. | 19×109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com