
分析 (1)根据方程有两个不相等的实数根,利用根的判别式结合二次项系数非0即可得出关于a的一元二次不等式,解不等式即可得出a的取值范围;
(2)根据根与系数的关系可得出x1+x2=-$\frac{2a-1}{{a}^{2}}$,结合方程的两个实数根互为相反数即可得出关于a的分式方程,解方程经检验后即可得出a值,结合(1)的结论即可得出不存在a的值使方程的两个实数根x1与x2互为相反数.
解答 解:(1)∵方程a2x2+(2a-1)x+1=0有两个实数根x1,x2,且x1≠x2,
∴$\left\{\begin{array}{l}{{a}^{2}≠0}\\{△=(2a-1)^{2}-4{a}^{2}>0}\end{array}\right.$,
解得:a<$\frac{1}{4}$且a≠0,
∴当a<$\frac{1}{4}$且a≠0时,方程有两个不相等的实数根.
(2)不存在,理由如下:
∵方程的两个实数根x1,x2互为相反数,
∴x1+x2=-$\frac{2a-1}{{a}^{2}}$=0,
解得:a=$\frac{1}{2}$,
经检验,a=$\frac{1}{2}$是方程-$\frac{2a-1}{{a}^{2}}$=0的根.
由①知:a≤$\frac{1}{4}$且a≠0时,方程才有两个实数根,
∵$\frac{1}{2}$>$\frac{1}{4}$,
∴不存在a的值使方程的两个实数根x1与x2互为相反数.
点评 本题考查了根的判别式以及根与系数的关系,根据方程解的个数结合根的判别式以及二次项系数非0得出关于a的不等式组是解题的关键.


科目:初中数学 来源: 题型:选择题
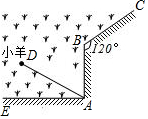 如图,一根3m的绳子,一端栓在柱子A上,另一端栓着一只羊,EABC为一墙,AB=2m,∠ABC=120°,则羊最大的活动区域的面积是( )
如图,一根3m的绳子,一端栓在柱子A上,另一端栓着一只羊,EABC为一墙,AB=2m,∠ABC=120°,则羊最大的活动区域的面积是( )| A. | $\frac{9}{4}$π | B. | 3π | C. | $\frac{29}{12}$π | D. | $\frac{1}{3}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知:如图所示,直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$交x轴于点A,交y轴于点B,若点P从点A出发,沿射线AB作匀速运动,点Q从点B出发,沿射线BO作匀速直线运动,两点同时出发,运动速度也相同,当△BPQ为直角三角形时,则点Q的坐标为(0,$\frac{\sqrt{3}}{3}$)或(0,-$\frac{\sqrt{3}}{3}$).
已知:如图所示,直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$交x轴于点A,交y轴于点B,若点P从点A出发,沿射线AB作匀速运动,点Q从点B出发,沿射线BO作匀速直线运动,两点同时出发,运动速度也相同,当△BPQ为直角三角形时,则点Q的坐标为(0,$\frac{\sqrt{3}}{3}$)或(0,-$\frac{\sqrt{3}}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com