
 (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+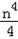 .(1)当n=1时,求点A的坐标;
.(1)当n=1时,求点A的坐标;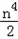 ,求OP2的最小值.
,求OP2的最小值.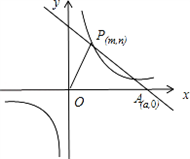
解:过点P作PQ⊥x轴于Q,则PQ=n,OQ=m,
(1)当n=1时,s= ,∴a=
,∴a=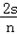 =
= .
.
∴A( ,0)
,0)
(2)解法一:
∵OP=AP,PA⊥OP,
∴△OPA是等腰直角三角形.
∴m=n= .
.
∴1+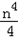 =
= an.
an.
即n4﹣4n2+4=0,
∴k2﹣4k+4=0,
∴k=2.
解法二:
∵OP=AP,PA⊥OP,
∴△OPA是等腰直角三角形.
∴m=n.
设△OPQ的面积为s1
则:s1= ×
× mn=
mn= (1+
(1+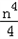 ),
),
即:n4﹣4n2+4=0,
∴k2﹣4k+4=0,
∴k=2.
(3)
∵PA⊥OP,PQ⊥OA,
∴△OPQ∽△OAP.
设:△OPQ的面积为s1,则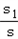 =
=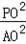
即: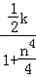 =
=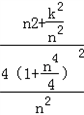 化简得:
化简得:
2n4+2k2﹣kn4﹣4k=0
(k﹣2)(2k﹣n4)=0,
∴k=2或k=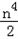 (舍去),
(舍去),
∴当n是小于20的整数时,k=2.
∵OP2=n2+m2=n2+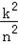 又m>0,k=2,
又m>0,k=2,
∴n是大于0且小于20的整数.
当n=1时,OP2=5,
当n=2时,OP2=5,
当n=3时,OP2=32+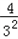 =9+
=9+ =
=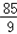 ,
,
当n是大于3且小于20的整数时,
即当n=4、5、6…19时,OP2的值分别是:
42+ 、52+
、52+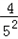 、62+
、62+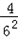 …192+
…192+ ,
,
∵192+ >182+
>182+ >32+
>32+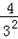 >5,
>5,
∴OP2的最小值是5.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
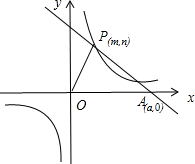 已知:O是坐标原点,P(m,n)(m>0)是函数y=
已知:O是坐标原点,P(m,n)(m>0)是函数y=| k |
| x |
| n4 |
| 4 |
| n4 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:第27章《相似》中考题集(15):27.2 相似三角形(解析版) 题型:解答题
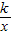 (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+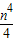 .
.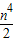 ,求OP2的最小值.
,求OP2的最小值.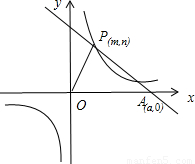
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《图形的相似》(04)(解析版) 题型:解答题
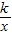 (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+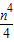 .
. ,求OP2的最小值.
,求OP2的最小值.
查看答案和解析>>
科目:初中数学 来源:2005年福建省厦门市中考数学试卷(课标卷)(解析版) 题型:解答题
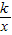 (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+ .
.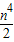 ,求OP2的最小值.
,求OP2的最小值.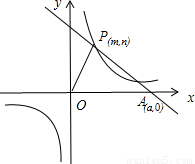
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com