
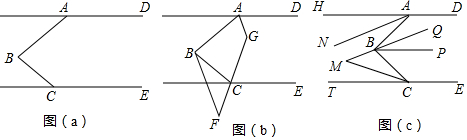
���� ��1���ȹ�B��BF��AD�����DAB+��ABF=180�㣬���ݡ�DAB+��ABC+��BCE=360�㣬��á�FBC+��BCE=360��-180��=180�㣬���ɵó�AD��CE��
��2���ȹ���G��GH��AD����GH��AD��CE������AG��CG�ֱ�ƽ�֡�BAD����BCE���Լ���DAB+��ABC+��BCE=360�㣬��á�AGC+$\frac{1}{2}$��ABC=180�㣬�ٸ���AG��BF����á�F+��AGC=180�㣬���ɵõ���ABC=2��F��
��3���ȸ���ANƽ�֡�HAB��BPƽ�֡�ABC��BQ��AN��CMƽ�֡�BCT���õ���QBP=��MCB���ٸ��ݡ�QBC�ǡ�BCM����ǣ��õ���QBC=��M+��MCB�������õ���M=$\frac{1}{2}$��ABC����$\frac{��QMC}{��ABC}$��ֵΪ$\frac{1}{2}$��
���  �⣺��1����B��BF��AD�����DAB+��ABF=180�㣬
�⣺��1����B��BF��AD�����DAB+��ABF=180�㣬
�ߡ�DAB+��ABC+��BCE=360�㣬
���FBC+��BCE=360��-180��=180�㣬
��BF��CE��
��AD��CE��
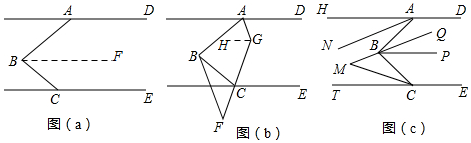
��2����ABC=2��F
֤��������G��GH��AD����GH��AD��CE��
���DAG=��AGH����HGC=��GCE��
��AG��CG�ֱ�ƽ�֡�BAD����BCE��
���AGC=$\frac{1}{2}$����DAB+��BCE����
�ߡ�DAB+��ABC+��BCE=360�㣬
��$\frac{1}{2}$����DAB+��ABC+��BCE��=180�㣬
����AGC+$\frac{1}{2}$��ABC=180�㣬
��AG��BF��
���F+��AGC=180�㣬
���ABC=2��F��
��3����$\frac{��QMC}{��ABC}$��ֵ���䣮
֤������������ۿɵã���ABC=��HAB+��TCB��
�֡�ANƽ�֡�HAB��BPƽ�֡�ABC��CMƽ�֡�BCT��
���ABP=��NAB+��MCB��
��BQ��AN��
���NAB=��ABQ��
���QBP=$\frac{1}{2}$��ABP=$\frac{1}{2}$��CBP=$\frac{1}{2}$��BCT=��MCB��
�ߡ�QBC�ǡ�BCM����ǣ�
���QBC=��M+��MCB��
���M=��QBC-��MCB=��QBC-��QBP=��PBC=$\frac{1}{2}$��ABC��
��$\frac{��QMC}{��ABC}$��ֵΪ$\frac{1}{2}$��
���� ������Ҫ������ƽ���ߵ��������ж�����������ǵ����ʵ��ۺ�Ӧ�ã�����ʱע�⣺ƽ���ߵ��ж����ɽǵ�������ϵ�ж���ֱ�ߵ�λ�ù�ϵ��ƽ���ߵ���������ƽ�й�ϵ��Ѱ�ҽǵ�������ϵ��Ӧ��ƽ���ߵ��ж������ʶ���ʱ��һ��ҪŪ������ͽ��ۣ���Ī������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
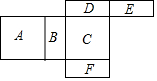 ��ͼ��һ�������չ��ͼ��ÿһ���ڶ���ע���֣�����ĸ����������棩������Ҫ��ش����⣺���D���ڶ���������棬��ôF�������
��ͼ��һ�������չ��ͼ��ÿһ���ڶ���ע���֣�����ĸ����������棩������Ҫ��ش����⣺���D���ڶ���������棬��ôF��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ֱ��x=0 | B�� | ֱ��x=2 | C�� | ֱ��x=4 | D�� | ֱ��x=-4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com