
分析 先把分母因式分解确定最简公分母,再进行通分,然后进行分式的加减运算得到原式=$\frac{-5x+1}{(x+1)(x-1)^{2}}$,再把x的值代入进行二次根式的混合运算即可.
解答 解:原式=$\frac{1}{x+1}$-$\frac{1}{(x+1)(x-1)}$-$\frac{x+1}{(x-1)^{2}}$
=$\frac{(x-1)^{2}-(x-1)-(x+1)^{2}}{(x+1)(x-1)^{2}}$
=$\frac{-5x+1}{(x+1)(x-1)^{2}}$,
当x=$\sqrt{3}$-1时,原式=$\frac{-5(\sqrt{3}-1)+1}{(\sqrt{3}-1+1)(\sqrt{3}-1-1)^{2}}$=$\frac{-5\sqrt{3}+6}{7\sqrt{3}-12}$=-11-6$\sqrt{3}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
 已知:如图,四边形ABCD是平行四边形.
已知:如图,四边形ABCD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在已建立直角坐标系的4×4正方形方格纸中,若每个小正方形的边长为1,将△ABC绕点B顺时针旋转90°到△DBE
如图,在已建立直角坐标系的4×4正方形方格纸中,若每个小正方形的边长为1,将△ABC绕点B顺时针旋转90°到△DBE 查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为π+$\frac{1}{2}$.
在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为π+$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
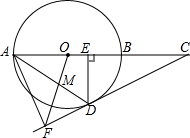 如图,AB为⊙O的直径,延长AB到点C,使得2BC=3OB,过点C作⊙O的切线,交⊙O于点D,过点D作DE⊥AC,连接AD,作∠DAF=∠CAD,交CD的延长线于点F.
如图,AB为⊙O的直径,延长AB到点C,使得2BC=3OB,过点C作⊙O的切线,交⊙O于点D,过点D作DE⊥AC,连接AD,作∠DAF=∠CAD,交CD的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 种植户 | 桃树种植面积(亩) | 牡丹种植面积(亩) | 销售总收入(元) |
| 甲 | 5 | 3 | 33500 |
| 乙 | 3 | 7 | 43500 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com