
| A. | $\sqrt{{x}^{2}+1}$ | B. | $\sqrt{{x}^{2}{y}^{3}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{\frac{1}{2}}$ |
分析 判定一个二次根式是不是最简二次根式的方法,就是逐个检查定义中的两个条件(①被开方数不含分母;②被开方数不含能开得尽方的因数或因式)是否同时满足,同时满足的就是最简二次根式,否则就不是.
解答 解:A、$\sqrt{{x}^{2}+1}$符合最简二次根式的条件;故本选项正确;
B、$\sqrt{{x}^{2}{y}^{3}}=xy\sqrt{y}$,被开方数里含有能开得尽方的因式;故本选项错误;
C、$\sqrt{12}=2\sqrt{3}$被开方数里含有能开得尽方的因数4;故本选项错误;
D、$\sqrt{\frac{1}{2}}$中被开方数里含有分母,故本选项错误.
故选A.
点评 本题主要考查了最简二次根式的定义,最简二次根式必须满足两个条件:
(1)被开方数不含分母;
(2)被开方数不含能开得尽方的因数或因式.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
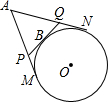 如图,A为⊙O外一点,AM、AN分别切⊙O于M、N点,PQ切⊙O于B,且交AM、AN分别于P、Q点.若AM=10,则△APQ的周长为20.
如图,A为⊙O外一点,AM、AN分别切⊙O于M、N点,PQ切⊙O于B,且交AM、AN分别于P、Q点.若AM=10,则△APQ的周长为20.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,不等长的两条对角线AC、BD相交于点O,且将四边形ABCD分成甲、乙、丙、丁四个三角形.若OA:OC=OB:OD=1:2,则甲、乙、丙、丁这4个三角形中,一定相似的有甲丙.
如图,不等长的两条对角线AC、BD相交于点O,且将四边形ABCD分成甲、乙、丙、丁四个三角形.若OA:OC=OB:OD=1:2,则甲、乙、丙、丁这4个三角形中,一定相似的有甲丙.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com