
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,求∠ABP的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
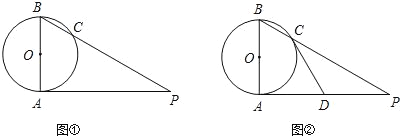
【答案】(1)55°;(2)证明见解析.
【解析】
(1)首先根据切线的性质判定∠BAP=90,然后利用直角三角形两锐角互余求出∠ABP;
(2)连接OC、OD、AC,证出∠OCD=90即可,由AB是直径,得到直角三角形ACP,根据直角三角形斜边上的中线等于斜边的一半得到CD=AD,从而△OAD≌△OCD,得到结论.
(1)解:∵AB是⊙O的直径,AP是⊙O的切线,
∴AB⊥AP,
∴∠BAP=90°;
又∵∠P=35°,
∴∠ABP=90°﹣35°=55°.
(2)证明:如图,连接OC,OD、AC.
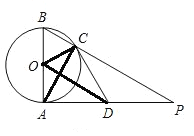
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),
∴∠ACP=90°;
又∵D为AP的中点,
∴AD=CD(直角三角形斜边上的中线等于斜边的一半);
在△OAD和△OCD中,
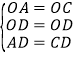 ,
,
∴△OAD≌△OCD(SSS),
∴∠OAD=∠OCD(全等三角形的对应角相等);
又∵AP是⊙O的切线,A是切点,
∴AB⊥AP,
∴∠OAD=90°,
∴∠OCD=90°,即直线CD是⊙O的切线.
故答案为:(1)55°;(2)证明见解析.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等.
(1)设A=![]() ,B=
,B=![]() ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,且CE=1,下列结论:①DM=CM;②![]() ;③⊙O的直径为2;④AE=AD.其中正确的结论有_____(填序号).
;③⊙O的直径为2;④AE=AD.其中正确的结论有_____(填序号).
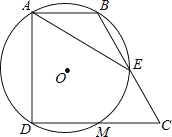
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,中俄“海上联合—2017”军事演习在海上编队演习中,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/小时的速度航行,二号舰以16海里/小时速度航行,离开港口1.5小时后它们分别到达A,B两点,相距30海里,则二号舰航行的方向是( )
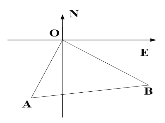
A. 南偏东30° B. 北偏东30° C. 南偏东 60° D. 南偏西 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )

A. BD=CE B. AD=AE C. DA=DE D. BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
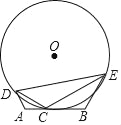
【题目】如图,已知线段AB=6,C为线段AB上的一个动点(不与A、B重合),将线段AC绕点A逆时针旋转120°得到AD,将线段BC绕点B顺时针旋转120°得到BE,⊙O外接于△CDE,则⊙O的半径最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
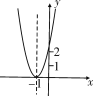
【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论是____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 为
为![]() 轴负半轴上一点,
轴负半轴上一点,![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标
点坐标![]() 为且
为且![]() .
.
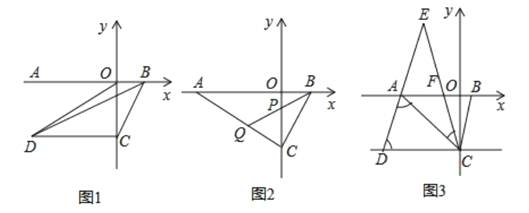
(1)求![]() 两点的坐标;
两点的坐标;
(2)求![]() ;
;
(3)如图2,若![]() 点坐标为
点坐标为![]() 点坐标为
点坐标为![]() ,点
,点![]() 为线段
为线段![]() 上一点,
上一点,![]() 的延长线交线段
的延长线交线段![]() 于点
于点![]() ,若
,若![]() ,求出点
,求出点![]() 坐标.
坐标.
(4)如图3,若![]() ,点
,点![]() 在
在![]() 轴正半轴上任意运动,
轴正半轴上任意运动,![]() 的平分线
的平分线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,在
,在![]() 点的运动过程中,
点的运动过程中,![]() 的值是否发生变化,若不变化,求出比值;若变化请说明理由.
的值是否发生变化,若不变化,求出比值;若变化请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com