
 如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,若EF的长为6$\sqrt{3}$,求AB的长.
如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,若EF的长为6$\sqrt{3}$,求AB的长. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
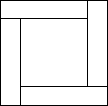 小明同学用四张长为x,宽为y的长方形卡片,拼出如图所示的包含两个正方形的图形(任意两张相邻的卡片之间没有重叠,没有空隙).
小明同学用四张长为x,宽为y的长方形卡片,拼出如图所示的包含两个正方形的图形(任意两张相邻的卡片之间没有重叠,没有空隙).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小敏不慎将一块矩形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的矩形玻璃,他带了两块碎玻璃,其编号应该是( )
小敏不慎将一块矩形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的矩形玻璃,他带了两块碎玻璃,其编号应该是( )| A. | ①② | B. | ?①③ | C. | ③④ | D. | ?②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com