
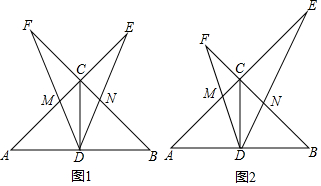
分析 (1)根据等腰直角三角形的性质得到∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,于是得到∠DCE=∠DCF=135°,根据全等三角形的性质即可的结论;
(2)①证得△CDF∽△CED,根据相似三角形的性质得到$\frac{CD}{CE}=\frac{CF}{CD}$,即CD2=CE•CF,根据等腰直角三角形的性质得到CD=$\frac{1}{2}$AB,于是得到AB2=4CE•CF;②如图,过D作DG⊥BC于G,于是得到∠DGN=∠ECN=90°,CG=DG,当CE=4,CF=2时,求得CD=2$\sqrt{2}$,推出△CEN∽△GDN,根据相似三角形的性质得到$\frac{CN}{GN}=\frac{CE}{DG}$=2,根据勾股定理即可得到结论.
解答  (1)证明:∵∠ACB=90°,AC=BC,AD=BD,
(1)证明:∵∠ACB=90°,AC=BC,AD=BD,
∴∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,
∴∠DCE=∠DCF=135°,
在△DCE与△DCF中,$\left\{\begin{array}{l}{CE=CF}\\{∠DCE=∠DCF}\\{CD=CD}\end{array}\right.$,
∴△DCE≌△DCF,
∴DE=DF;
(2)解:①∵∠DCF=∠DCE=135°,
∴∠CDF+∠F=180°-135°=45°,
∵∠CDF+∠CDE=45°,
∴∠F=∠CDE,
∴△CDF∽△CED,
∴$\frac{CD}{CE}=\frac{CF}{CD}$,
即CD2=CE•CF,
∵∠ACB=90°,AC=BC,AD=BD,
∴CD=$\frac{1}{2}$AB,
∴AB2=4CE•CF;
②如图,过D作DG⊥BC于G,
则∠DGN=∠ECN=90°,CG=DG,
当CE=4,CF=2时,
由CD2=CE•CF得CD=2$\sqrt{2}$,
∴在Rt△DCG中,CG=DG=CD•sin∠DCG=2$\sqrt{2}$×sin45°=2,
∵∠ECN=∠DGN,∠ENC=∠DNG,
∴△CEN∽△GDN,
∴$\frac{CN}{GN}=\frac{CE}{DG}$=2,
∴GN=$\frac{1}{3}$CG=$\frac{2}{3}$,
∴DN=$\sqrt{G{N}^{2}+D{G}^{2}}$=$\sqrt{(\frac{2}{3})^{2}+{2}^{2}}$=$\frac{2\sqrt{10}}{3}$.
点评 本题考查了旋转的性质,全等三角形的判定和性质,相似三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线是解题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
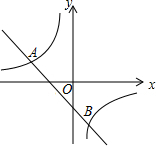 如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)交于点A(-4,n)和点B(2,-4).
如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)交于点A(-4,n)和点B(2,-4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
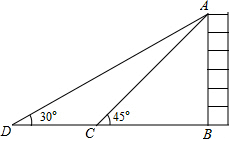 如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为137米.
如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为137米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,C城市在A城市正东方向,现计划在A、C两城市间修建一条高速公路(即线段AC),经测量,森林保护区的中心P在A城市的北偏东60°方向上,在线段AC上距A城市120km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100km为半径的圆形区域,请问计划修建的这条高速公路是否穿越保护区,为什么?(参考数据:$\sqrt{3}$≈1.73)
如图所示,C城市在A城市正东方向,现计划在A、C两城市间修建一条高速公路(即线段AC),经测量,森林保护区的中心P在A城市的北偏东60°方向上,在线段AC上距A城市120km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100km为半径的圆形区域,请问计划修建的这条高速公路是否穿越保护区,为什么?(参考数据:$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 尺规作图(不写作法,保留作图痕迹):
尺规作图(不写作法,保留作图痕迹):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com