

分析 (1)首先证明△MIP≌△MIQ,得到∠MPI=∠MQI,推出∠IPS=∠IQT,由∠IPN=∠IQN,∠IPN=∠IPS,即可证明.
(2)先证明△PIE≌△PIN,同理可证△QIN≌△QIF,创造条件证明△MIE≌△MIF即可.
解答 证明:(1)如图甲中,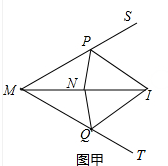
∵△PMN≌△QMN,
∴PM=QM,∠PMN=∠QMN,∠MPN=∠MQN,
∴∠SPN=∠TQN,
在△PMI和△QMI中,
$\left\{\begin{array}{l}{PM=QM}\\{∠PMI=∠QMI}\\{MI=MI}\end{array}\right.$,
∴△PMI≌△QMI,
∴∠MPI=∠MQI,
∴∠IPN=∠IQN,
∵∠IPS=∠IPN,
∴∠IPS=∠IQT=∠IQN,
∴IQ平分∠TQN.
(2)如图乙中,在PS上截取PE=PN,在QT上JQ NQ=QF,连接EI、IN、IT.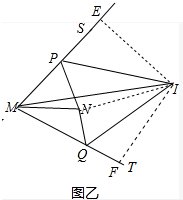
在△PIE和△PIN中,
$\left\{\begin{array}{l}{PI=PI}\\{∠IPE=∠IPN}\\{PE=PN}\end{array}\right.$,
∴△PIE≌△PIN,同理可证△QIN≌△QIF,
∴IE=IN=IT,
∵PM+PN=QM+QN,
∴PM+PE=MQ+QF即ME=MF,
在△MIE和△MIF中,
$\left\{\begin{array}{l}{MI=MI}\\{ME=MF}\\{IE=IF}\end{array}\right.$,
∴△MIE≌△MIF,
∴∠IME=∠IMF,
∴MI平分∠PMQ.
点评 本题考查全等三角形的判定和性质、角平分线、三角形外角等知识,解题的关键是学会添加辅助线,构造全等三角形,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
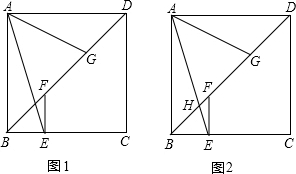
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
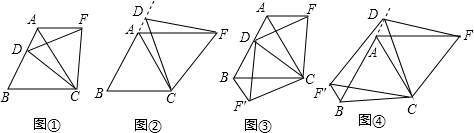
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1≤y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
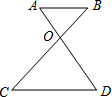 如图AB∥CD,AD、BC交于O点,则下列各式:
如图AB∥CD,AD、BC交于O点,则下列各式:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com