
分析 (1)根据已知条件求得C点的坐标,进而根据待定系数法即可求得;
(2)根据平行于BC的直线与抛物线只有一个交点时△BEF的面积最大,先求出直线BC的解析式为y=x+2,再设出平行于直线BC的直线的解析式y=x+b,然后与抛物线联立,消掉未知数y,得到关于x的一元二次方程,利用根的判别式△=0列式求出b值,再求出点P的坐标;
(3)设G点(x,-$\frac{1}{2}$x2+$\frac{3}{2}$x+5)(-2<x<0),根据S△BEG=S梯形GHAB-S梯形GHOE-S梯形EOAB得出S△BEG=-$\frac{3}{4}$x2+$\frac{3}{4}$x+$\frac{9}{2}$=3,再解方程即可;
(4)求得直线CM和ED的解析式,然后分三种情况分别讨论即可求得.
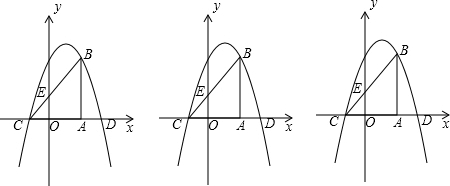
解答 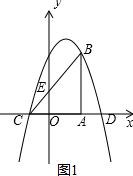 解:(1)如图1,∵△ABC是等腰直角三角形,∠CAB=90°,
解:(1)如图1,∵△ABC是等腰直角三角形,∠CAB=90°,
∴AB∥y轴,
∵B(3,5),
∴AC=AB=5,OA=3,
∴OC=2,
∴C(-2,0),
∵抛物线y=-$\frac{1}{2}$x2+bx+c交x轴于C、D两点,且经过点B.
∴$\left\{\begin{array}{l}{5=-\frac{9}{2}+3b+c}\\{0=-2-2b+c}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=\frac{3}{2}}\\{c=5}\end{array}\right.$,
∴抛物线的表达式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+5;
(2)根据三角形的面积,当平行于BC的直线与抛物线只有一个交点时△BEF的面积最大,
∵B(3,5),C(-2,0),
∴直线BC为y=x+2,
∴E(0,2),
设与直线BC平行的直线为y=x+b,
联立$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+\frac{3}{2}x+5}\\{y=x+b}\end{array}\right.$,
消掉y得,x2-x+2b-10=0,
△=(-1)2-4×1×(2b-10)=0,
即b=$\frac{41}{8}$时,直线与抛物线只有一个交点,△BEF的面积最大,此时,x=-$\frac{-1}{2×1}$=$\frac{1}{2}$,
y=$\frac{1}{2}$+$\frac{41}{8}$=$\frac{45}{8}$,
所以,点F的坐标为($\frac{1}{2}$,$\frac{45}{8}$),
(2)如图:设G点(x,-$\frac{1}{2}$x2+$\frac{3}{2}$x+5)(-2<x<0)
则S△BEG=S梯形GHAB-S梯形GHOE-S梯形EOAB
=$\frac{1}{2}$(GH+AB)•AH-$\frac{1}{2}$(GH+OE)•OH-$\frac{1}{2}$(OE+AB)•OA=$\frac{1}{2}$(-$\frac{1}{2}$x2+$\frac{3}{2}$x+5+5)(-x+3)-$\frac{1}{2}$(-$\frac{1}{2}$x2+$\frac{3}{2}$x+5+2)(-x)-$\frac{1}{2}$(2+5)×3=-$\frac{3}{4}$x2+$\frac{3}{4}$x+$\frac{9}{2}$,
若△BEG的面积等于3,则-$\frac{3}{4}$x2+$\frac{3}{4}$x+$\frac{9}{2}$=3
解得:x1=-1,x2=2(舍去),
当x=1时,y=3,
则G点的坐标是(-1,3);
(4)∵点M(4,K)在抛物线上,
∴K=-$\frac{1}{2}$×16+$\frac{3}{2}$×4+5=3,
∴M(4,3),
∵C(-2,0),
∴直线CM的解析式为y=$\frac{1}{2}$x+1,
令-$\frac{1}{2}$x2+$\frac{3}{2}$x+5=0,解得x=-2或5,
∴D(5,0),
∵E(0,2),
∴直线ED的解析式为y=-$\frac{2}{5}$x+2,
①当∠EDP=90°时,设直线PD的解析式为y=$\frac{5}{2}$x+n,
把D(5,0)代入得,0=$\frac{5}{2}$×5+n,
∴n=-$\frac{25}{2}$,
∴直线PD的解析式为y=$\frac{5}{2}$x-$\frac{25}{2}$,
解$\left\{\begin{array}{l}{y=\frac{5}{2}x-\frac{25}{2}}\\{y=\frac{1}{2}x+1}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{27}{4}}\\{y=\frac{35}{8}}\end{array}\right.$,
∴P($\frac{27}{4}$,$\frac{35}{8}$);
②当∠DPE=90°时,设P(x,$\frac{1}{2}$x+1),
∴x2+($\frac{1}{2}$x+1-2)2+(x-5)2+($\frac{1}{2}$x+1)2=22+52,
解得,x=2±$\frac{2\sqrt{30}}{5}$,
∴P(2+$\frac{2}{5}$$\sqrt{30}$,2+$\frac{4}{5}$$\sqrt{30}$)或(2-$\frac{2}{5}$$\sqrt{30}$,2-$\frac{4}{5}$$\sqrt{30}$);
③当∠PED=90°时,直线PE的解析式为y=$\frac{5}{2}$x+m,
把E(0,2)代入得,m=2,
∴直线PD的解析式为y=$\frac{5}{2}$x+2,
解$\left\{\begin{array}{l}{y=\frac{5}{2}x+2}\\{y=\frac{1}{2}x+1}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{3}{4}}\end{array}\right.$,
∴P(-$\frac{1}{2}$,$\frac{3}{4}$);
综上,使△DEP是直角三角形的P点的坐标为($\frac{27}{4}$,$\frac{35}{8}$)或(2+$\frac{2}{5}$$\sqrt{30}$,2+$\frac{4}{5}$$\sqrt{30}$)或(2-$\frac{2}{5}$$\sqrt{30}$,2-$\frac{4}{5}$$\sqrt{30}$)或(-$\frac{1}{2}$,$\frac{3}{4}$).
点评 本题是二次函数的综合题,考查了待定系数法求二次函数的解析式、梯形的面积公式、一次函数、二次函数的图象和性质,注意数形结合思想和分类讨论思想的应用.


 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| -1.6 | -1.2 | -1 | 0 | 1.2 | 1.4 | 1.8 |
| 1 | 5 | 4 | 8 | 6 | 4 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
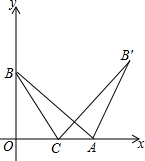 如图,在平面直角坐标系xOy中,点A、B分别在x轴,y轴的正半轴上,且OA=OB,将线段AB绕点A顺时针旋转60°得到AB′,C是x轴上一点,BC+B′C的值最小是B′D,∠OCB=60°.
如图,在平面直角坐标系xOy中,点A、B分别在x轴,y轴的正半轴上,且OA=OB,将线段AB绕点A顺时针旋转60°得到AB′,C是x轴上一点,BC+B′C的值最小是B′D,∠OCB=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com