
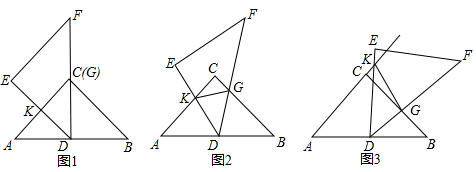
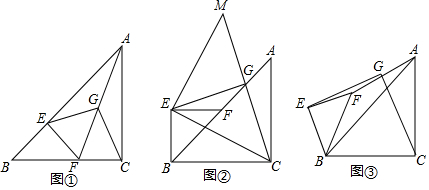
·ÖĪö Ģ½¾æ1£¬øł¾Ż”÷ABC”¢”÷DEFŹĒµČŃüÖ±½ĒČż½ĒŠĪæÉÖŖ”ĻKAD=”ĻKDG=”ĻDBG=45”ć£¬ÓÉČż½ĒŠĪÄŚ½ĒŗĶ¶ØĄķæÉÖŖ”ĻKDA+”ĻBDG=135”ć£®”ĻBDG+”ĻBGD=135”ć£¬¹ŹæÉµĆ³ö”÷ADK”×”÷BGD£»
Ģ½¾æ2£¬øł¾Ż”÷ADK”×”÷BGDæÉÖŖ$\frac{AK}{BD}=\frac{KD}{BD}$£¬ŌŁÓɵćDŹĒĻ߶ĪABµÄÖŠµćµĆ³öBD=AD£¬¹ŹæÉµĆ³ö”÷ADK”×”÷DCK£¬”ĻAKD=”ĻDKC£¬ÓÉ“ĖæÉµĆ³ö½įĀŪ£»
Ģ½¾æ3£¬¢ŁĶ¬Ģ½¾æ1æɵƔ÷ADK”×”÷BGD£¬Ķ¬Ģ½¾æ2æÉµĆ£¬”÷ADK”×”÷DGK£¬¹ŹæÉµĆ³ö½įĀŪ£»
¢Ś¹żµćD×÷DM”ĶACÓŚµćM£¬DN”ĶKGÓŚµćN£¬ÓÉ¢ŁÖŖĻ߶ĪKDĘ½·Ö”ĻAKG£¬¹ŹDM=DN£®ŌŁÓÉAC=BC=8£¬µćDŹĒĻ߶ĪABµÄÖŠµć£¬”ĻKAD=45”ć£¬æÉÖŖDM=DN=4£®øł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½¼“æÉµĆ³ö½įĀŪ£®
½ā“š ½ā£ŗĢ½¾æ1£¬
”ß”ĻKAD=”ĻKDG=”ĻDBG=45”ć£¬
”ą”ĻKDA+”ĻBDG=135”ć£®
”ß”ĻBDG+”ĻBGD=135”ć£¬
”ą”ĻKDA=”ĻBGD£¬
”ą”÷ADK”×”÷BGD£»
Ģ½¾æ2£¬”ß”÷ADK”×”÷BGD£¬
”ą$\frac{AK}{BD}$=$\frac{KD}{DG}$£¬
”ßµćDŹĒĻ߶ĪABµÄÖŠµć£¬
”ąBD=AD£¬
”ą$\frac{AK}{AD}$=$\frac{KD}{DG}$£¬
”ą$\frac{AK}{KD}$=$\frac{AD}{DG}$£¬
”ß”ĻKAD=”ĻKDG=45”ć£¬
”ą”÷ADK”×”÷DCK£¬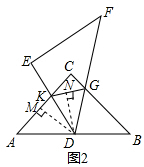
”ą”ĻAKD=”ĻDKC£¬
”ąKDĘ½·Ö”ĻAKG£»
Ģ½¾æ3£¬¢ŁKDČŌĘ½·Ö”ĻAKG£®
ĄķÓÉČēĻĀ£ŗ
”ßĶ¬Ģ½¾æ1æɵƔ÷ADK”×”÷BGD£¬
Ķ¬Ģ½¾æ2æÉµĆ£¬”÷ADK”×”÷DGK£¬
”ą”ĻAKD=”ĻDKG£¬
”ąKDČŌĘ½·Ö”ĻAKG£»
¢ŚČēĶ¼£¬¹żµćD×÷DM”ĶACÓŚµćM£¬DN”ĶKGÓŚµćN£¬
ÓÉ¢ŁÖŖĻ߶ĪKDĘ½·Ö”ĻAKG£¬
”ąDM=DN£®
”ßAC=BC=8£¬µćDŹĒĻ߶ĪABµÄÖŠµć£¬”ĻKAD=45”ć£¬
”ąDM=DN=4£®
”ßKG=3£¬
”ąS”÷DKG=$\frac{1}{2}$”Į4”Į3=6£®
µćĘĄ ±¾Ģāæ¼²éµÄŹĒĻąĖĘŠĪ×ŪŗĻĢā£¬Éę¼°µ½ĻąĖĘČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ”¢µČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµČÖŖŹ¶£®ÄѶȏŹÖŠ£®


 ÖŠæ¼½ā¶Įæ¼µć¾«Į·ĻµĮŠ“š°ø
ÖŠæ¼½ā¶Įæ¼µć¾«Į·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
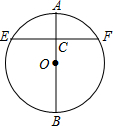 ČēĶ¼£¬ŌŚ”ŃOÖŠ£¬Ö±¾¶ABµÄ³¤¶ČĪŖ4a£¬3AC=CB£¬¹żµćC×÷EF”ĶAB£¬½»”ŃOÓŚµćE£¬F£¬ŌņEFµÄ³¤¶ČĪŖ2$\sqrt{3}$a£®
ČēĶ¼£¬ŌŚ”ŃOÖŠ£¬Ö±¾¶ABµÄ³¤¶ČĪŖ4a£¬3AC=CB£¬¹żµćC×÷EF”ĶAB£¬½»”ŃOÓŚµćE£¬F£¬ŌņEFµÄ³¤¶ČĪŖ2$\sqrt{3}$a£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
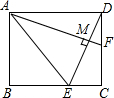 ČēĶ¼ĖłŹ¾£¬ŌŚ¾ŲŠĪABCDÖŠ£¬FŹĒDCÉĻµÄŅ»µć£¬AEĘ½·Ö”ĻBAF½»BCÓŚµćE£¬ĒŅDE”ĶAF£¬“¹×ćĪŖµćM£¬BE=3£¬AE=2$\sqrt{6}$£¬ŌņMDµÄ³¤ŹĒ£Ø””””£©
ČēĶ¼ĖłŹ¾£¬ŌŚ¾ŲŠĪABCDÖŠ£¬FŹĒDCÉĻµÄŅ»µć£¬AEĘ½·Ö”ĻBAF½»BCÓŚµćE£¬ĒŅDE”ĶAF£¬“¹×ćĪŖµćM£¬BE=3£¬AE=2$\sqrt{6}$£¬ŌņMDµÄ³¤ŹĒ£Ø””””£©| A£® | $\sqrt{15}$ | B£® | $\frac{{\sqrt{15}}}{15}$ | C£® | 1 | D£® | $\frac{{\sqrt{15}}}{10}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com