
分析 (1)先分别根据绝对值的性质、特殊角的三角函数值、负整数指数幂的计算法则分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)原式=2-3+4×$\frac{\sqrt{2}}{2}$
=-1+2$\sqrt{2}$;
(2)$\left\{\begin{array}{l}2(x+2)≤3x+3①\\ \frac{x}{3}<\frac{x+1}{4}②\end{array}\right.$,
由①得,x≥1,
由②得,x<3,
故不等式组的解集为:1≤x<3.
点评 本题考查的是实数的运算,熟知绝对值的性质、特殊角的三角函数值及负整数指数幂的计算法则是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
 在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为5•($\frac{3}{2}$)4022.
在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为5•($\frac{3}{2}$)4022.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)在所给平面直角坐标系中,画出反比例函数y=$\frac{4}{x}$的图象;
(1)在所给平面直角坐标系中,画出反比例函数y=$\frac{4}{x}$的图象;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
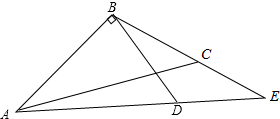 已知,如图,△ABC中,BD⊥AB于点B,AD的延长线交BC于点E.若∠CAE=∠CBD,∠EAB-∠BCA=10°,求出∠BAD的度数.
已知,如图,△ABC中,BD⊥AB于点B,AD的延长线交BC于点E.若∠CAE=∠CBD,∠EAB-∠BCA=10°,求出∠BAD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com