
分析 连接AF、OF,延长CO交EF于点H,先证明AB是△AOB的外接圆的直径,得出∠AFB=90°=∠AFC,由ASA证明△AEF≌△OFA,得出EF=OA=OC,再由等腰三角形的性质和三角形内角和定理得出∠CHF=90°即可.
解答 证明:连接AF、OF,延长CO交EF于点H,如图所示: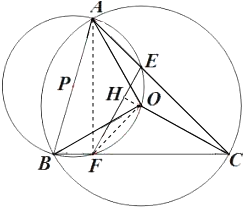 ∵∠ACB=45°,O为外心,
∵∠ACB=45°,O为外心,
∴∠AOB=2∠ACB=90°,OA=OB=CO,
∴AB是△AOB的外接圆的直径,∠AFO=45°=∠ABO,
∴∠AFB=90°=∠AFC,
∴AF=CF,∠CFO=45°=∠AFO=∠CAF=∠OFC,
∵∠OAE=∠OFE,
∴∠OAF=∠EFA,
在△AEF和△OFA中,$\left\{\begin{array}{l}{∠OAF=∠EFA}\\{AF=AF}\\{∠AFO=∠EAF}\end{array}\right.$,
∴△AEF≌△OFA(ASA),
∴EF=OA=CO,
∵OB=OC,
∴∠OCB=∠OBC=∠OAF,
∴∠CHF=180°-(∠HOF+∠OFE)=180°-(∠OFC+∠OCF+∠OFE)
=180°-(∠OFC+∠OAF+∠OAE)=180°-(∠OFC+∠EAF)
=180°-(45°+45°)=90°,
∴OC⊥EF.
点评 本题考查了圆周角定理、全等三角形的判定与性质、等腰三角形的判定与性质;本题综合性强,有一定难度,需要通过作辅助线才能得出结论.


科目:初中数学 来源: 题型:解答题
 如图所示是我市企业职工养老保险个人月缴费y(元)随个人工资x(元)变化的图象,请你根据图象回答下面的问题:
如图所示是我市企业职工养老保险个人月缴费y(元)随个人工资x(元)变化的图象,请你根据图象回答下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
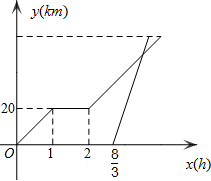 暑假期间,小亮骑自行车从家里出去旅游,从家出发一小时后到达甲地,游玩一段时间后,按元素前往乙地,小亮离家2小时40分钟后,爸爸驾车沿相同录像前往乙地,如图是他们离家的路程y(km)与小亮离家时间x(h)的函数图象,已知爸爸驾车的速度是小亮骑车速度的3倍.
暑假期间,小亮骑自行车从家里出去旅游,从家出发一小时后到达甲地,游玩一段时间后,按元素前往乙地,小亮离家2小时40分钟后,爸爸驾车沿相同录像前往乙地,如图是他们离家的路程y(km)与小亮离家时间x(h)的函数图象,已知爸爸驾车的速度是小亮骑车速度的3倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com