
【题目】如图,已知四边形ABCD是矩形,点P在BC边的延长线上,且PD=BC,⊙A经过点B,与AD边交于点E,连接CE .
(1)求证:直线PD是⊙A的切线;
(2)若PC=2![]() ,sin∠P=
,sin∠P=![]() ,求图中阴影部份的面积(结果保留无理数).
,求图中阴影部份的面积(结果保留无理数).
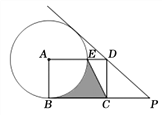
【答案】(1)见解析;(2)20-4π.
【解析】分析:(1)过点A作AH⊥PD,垂足为H,只要证明AH为半径即可.
(2)分别算出Rt△CED的面积,扇形ABE的面积,矩形ABCD的面积即可.
详解:(1)证明:如图,过A作AH⊥PD,垂足为H,
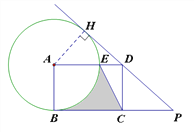
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∠PCD=∠BCD=90°,
∴∠ADH=∠P,∠AHD=∠PCD=90°,
又PD=BC,∴AD=PD,
∴△ADH≌△DPC,∴AH=CD,
∵CD=AB,且AB是⊙A的半径,
∴AH=AB,即AH是⊙A的半径,
∴PD是⊙A的切线.
(2)如图,在Rt△PDC中,∵sin∠P=![]() ,PC=2
,PC=2![]() ,
,
令CD=2x,PD=3x,由由勾股定理得:(3x)2-(2x)2=(2![]() )2,
)2,
解得:x=2,∴CD=4,PD=6,
∴AB=AE=CD=4,AD=BC=PD=6,DE=2,
∵矩形ABCD的面积为6×4=24,Rt△CED的面积为![]() ×4×2=4,
×4×2=4,
扇形ABE的面积为![]() π×42=4π,
π×42=4π,
∴图中阴影部份的面积为24-4-4π=20-4π.


科目:初中数学 来源: 题型:
【题目】某家具厂生产一种餐桌和椅子,餐桌每张定价为![]() 元,椅子每把定价为
元,椅子每把定价为![]() 元,厂方在开展促销活动期间,向客户提供两种优惠方案:
元,厂方在开展促销活动期间,向客户提供两种优惠方案:
方案一:每买一张餐桌就赠送一把椅子;
方案二:餐桌和椅子都按定价的![]() 付款.
付款.
某餐厅计划添置![]() 张餐桌和
张餐桌和![]() 把椅子.
把椅子.
(1)若![]() ,请用含
,请用含![]() 的代数式分别把两种方案的费用表示出来.
的代数式分别把两种方案的费用表示出来.
(2)已知![]() ,如果两种方案可以同时使用,请帮助餐厅设计一种最省钱的方案.
,如果两种方案可以同时使用,请帮助餐厅设计一种最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,动点P在∠ABC的平分线BD上,动点M在BC边上,若BC=3,∠ABC=45°,则PM+PC的最小值是( )

A. 2 B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况,随机抽样调查了某校初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,回答下列问题:

(1)扇形统计图中a的值为_____,“活动时间为4天”的扇形所对圆心角的度数为_____°,该校初一学生的总人数为______;
(2)补全频数分布直方图;
(3)如果该市共有初一学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=![]() AB时,求t的值.
AB时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
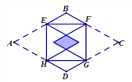
【题目】如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH, △CFG分别沿EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的![]() 时,则
时,则![]() 为( )
为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
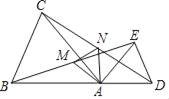
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在同一条直线上,M,N分别为BE,CD的中点.
(1)求证:△ABE≌ACD;
(2)判断△AMN的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com