
 如图,点A,B,C,D都在⊙O上,
如图,点A,B,C,D都在⊙O上, |
| CD |
| 1 |
| 2 |
| 1 |
| 2 |
 |
| CD |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、(0,-3) |
| B、(-4,-3) |
| C、(0,-9) |
| D、(-4,-9) |
查看答案和解析>>
科目:初中数学 来源: 题型:
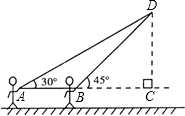 放风筝是广受喜爱的一种运动,星期天的上午小明在大运河广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树捎上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°.为了便于观察,小明迅速向前边移动边收线到达了B处,此时风筝BD与水平线的夹角为45°.已知点A、B、C在同一条直线上,∠ACD=90°,点B距大树CD的水平距离为8米.请你求出小明此时所收回的风筝线的长度是多少米?(结果保留根号)
放风筝是广受喜爱的一种运动,星期天的上午小明在大运河广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树捎上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°.为了便于观察,小明迅速向前边移动边收线到达了B处,此时风筝BD与水平线的夹角为45°.已知点A、B、C在同一条直线上,∠ACD=90°,点B距大树CD的水平距离为8米.请你求出小明此时所收回的风筝线的长度是多少米?(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com