
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标,若不存在,请说明理由.

【答案】(1)![]() ;(2)△BCM是Rt△;(3)O(0,0),P1(0,
;(2)△BCM是Rt△;(3)O(0,0),P1(0, ![]() ),P2(9,0).
),P2(9,0).
【解析】试题分析:(1)已知抛物线图象上的三点坐标,可用待定系数法求出该抛物线的解析式;
(2)根据B、C、M的坐标,可求得△BCM三边的长,然后判断这三条边的长是否符合勾股定理即可;
(3)假设存在符合条件的P点;首先连接AC,根据A、C的坐标及(2)题所得△BDC三边的比例关系,即可判断出点O符合P点的要求,因此以P、A、C为顶点的三角形也必与△COA相似,那么分别过A、C作线段AC的垂线,这两条垂线与坐标轴的交点也符合点P点要求,可根据相似三角形的性质(或射影定理)求得OP的长,也就得到了点P的坐标.
解:(1)∵二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,
∴![]() ,
,
解得:![]() ,
,
则抛物线解析式为y=x2﹣2x﹣3;
(2)△BCM为直角三角形,理由为:
对于抛物线解析式y=x2﹣2x﹣3=(x﹣1)2﹣4,即顶点M坐标为(1,﹣4),
令x=0,得到y=﹣3,即C(0,﹣3),
根据勾股定理得:BC=3![]() ,BM=2
,BM=2![]() ,CM=
,CM=![]() ,
,
∵BM2=BC2+CM2,
∴△BCM为直角三角形;
(3)若∠APC=90°,即P点和O点重合,如图1,
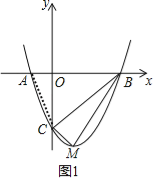
连接AC,
∵∠AOC=∠MCB=90°,且![]() =
=![]() ,
,
∴Rt△AOC∽Rt△MCB,
∴此时P点坐标为(0,0).
若P点在y轴上,则∠PAC=90°,如图2,过A作AP1⊥AC交y轴正半轴于P1,
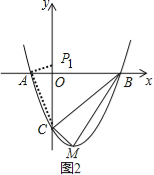
∵Rt△CAP1∽Rt△COA∽Rt△BCM,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴点P1(0,![]() ).
).
若P点在x轴上,则∠PCA=90°,如图3,过C作CP2⊥AC交x轴正半轴于P2,
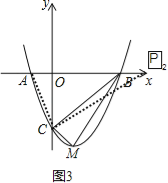
∵Rt△P2CA∽Rt△COA∽Rt△BCM,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,AP2=10,
,AP2=10,
∴点P2(9,0).
∴符合条件的点有三个:O(0,0),P1(0,![]() ),P2(9,0).
),P2(9,0).


科目:初中数学 来源: 题型:
【题目】某一次函数的图象经过点(1,2),且y随x的增大而减小,则这个函数的表达式可能是
A. y=-2x+4 B. y=3x-1 C. y=-3x+1 D. y=2x+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.周长相等的锐角三角形都全等
B.周长相等的直角三角形都全等
C.周长相等的钝角三角形都全等
D.周长相等的等腰直角三角形都全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你一定知道乌鸦喝水的故事吧!一个紧口瓶中盛有一些水,乌鸦想喝,但是嘴够不着瓶中的水,于是乌鸦衔来一些小石子放入瓶中,瓶中水面的高度随石子的增多而上升,乌鸦喝到了水.但是还没解渴,瓶中水面就下降到乌鸦够不着的高度,乌鸦只好再去衔些石子放入瓶中,水面又上升,乌鸦终于喝足了水,哇哇地飞走了.如果设衔入瓶中石子的体积为x,瓶中水面的高度为Y,下面能大致表示上面故事情节的图象是( )
A.
B.
C.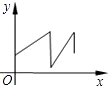
D.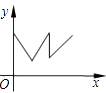
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为420米,求这栋楼的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC内接于⊙0,连接AO并延长交BC于点D.

(l)如图l,求证:∠ABC+∠CAD=90°;
(2)如图2,过点D作DE⊥AB于E,若∠ADC=2∠ACB.求证:AC=2DE;
(3)如图3,在(2)的条件下,连接BO交DE于点F,延长ED交⊙0于点G,连接AG,若AC=![]() ,BF=OD,求线段AG的长.
,BF=OD,求线段AG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com