
分析 根据相似三角形的对应边的比等于相似比列出比例式,计算即可.
解答 解:∵△ABC∽△A1B1C1,相似比为$\frac{2}{3}$,
∴$\frac{AB}{{A}_{1}{B}_{1}}$=$\frac{BC}{{B}_{1}{C}_{1}}$=$\frac{AC}{{A}_{1}{C}_{1}}$=$\frac{2}{3}$,即$\frac{4}{{A}_{1}{B}_{1}}$=$\frac{5}{{B}_{1}{C}_{1}}$=$\frac{AC}{9}$=$\frac{2}{3}$,
解得,A1B1=6,B1C1=7.5,AC=6.
点评 本题考查的是相似三角形的性质,掌握相似三角形的对应边的比等于相似比是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
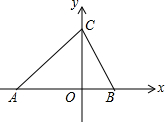 如图,在平面直角坐标系中,A(-4,0),B(2,0),点C在y轴正半轴上,且S△ABC=18.
如图,在平面直角坐标系中,A(-4,0),B(2,0),点C在y轴正半轴上,且S△ABC=18.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年龄x | 生存人数l | 死亡人数d |
| 0 | 1000000 | 661 |
| 1 | 999339 | 536 |
| 30 | 991476 | 403 |
| 31 | 991074 | 428 |
| 61 | 938005 | 6064 |
| 62 | 931941 | 6743 |
| 63 | 925198 | 7489 |
| 64 | 917709 | 8314 |
| 79 | 649175 | 32429 |
| 80 | 616746 | 34398 |
| 81 | 582347 | 36253 |
| 82 | 546095 | 37950 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com