
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(-4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO.
如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(-4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
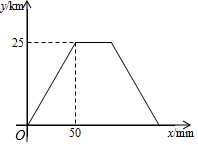 甲、乙两人骑车分别从A、B两地同时出发,沿同一路线匀速骑行,两人先相向而行,甲到达B地后停留20min再以原速返回A地,当两人到达A地后停止骑行.设甲出发xmin后距离A地的路程为ykm.图中的折线表示甲在整个骑行过程中y与x的函数关系.
甲、乙两人骑车分别从A、B两地同时出发,沿同一路线匀速骑行,两人先相向而行,甲到达B地后停留20min再以原速返回A地,当两人到达A地后停止骑行.设甲出发xmin后距离A地的路程为ykm.图中的折线表示甲在整个骑行过程中y与x的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
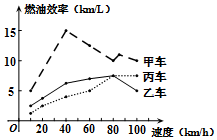 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )| A. | 当行驶速度为40km/h时,每消耗1升汽油,甲车能行驶20km | |
| B. | 消耗1升汽油,丙车最多可行驶5km | |
| C. | 当行驶速度为80km/h时,每消耗1升汽油,乙车和丙车行驶的最大公里数相同 | |
| D. | 当行驶速度为60km/h时,若行驶相同的路程,丙车消耗的汽油最少 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
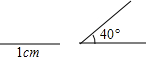 已知一个三角形的两条边长分别是1cm和2cm,一个内角为40°(请在图中标出已知角的度数和已知边的长度,用直尺和圆规作图时,不写作法,保留作图痕迹).
已知一个三角形的两条边长分别是1cm和2cm,一个内角为40°(请在图中标出已知角的度数和已知边的长度,用直尺和圆规作图时,不写作法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com