
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.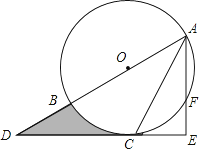
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
【答案】
(1)
证明:连接OC,
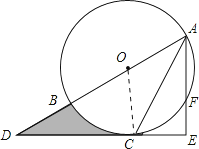
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠BAE,
∴∠OAC=∠CAE,
∴∠OCA=∠CAE,
∴OC∥AE,
∴∠OCD=∠E,
∵AE⊥DE,
∴∠E=90°,
∴∠OCD=90°,
∴OC⊥CD,
∵点C在圆O上,OC为圆O的半径,
∴CD是圆O的切线
(2)
解:在Rt△AED中,
∵∠D=30°,AE=6,
∴AD=2AE=12,
在Rt△OCD中,∵∠D=30°,
∴DO=2OC=DB+OB=DB+OC,
∴DB=OB=OC= ![]() AD=4,DO=8,
AD=4,DO=8,
∴CD= ![]() =
= ![]() =4
=4 ![]() ,
,
∴S△OCD= ![]() =8
=8 ![]() ,
,
∵∠D=30°,∠OCD=90°,
∴∠DOC=60°,
∴S扇形OBC= ![]() ×π×OC2=
×π×OC2= ![]() ,
,
∵S阴影=S△COD﹣S扇形OBC
∴S阴影=8 ![]() ﹣
﹣ ![]() ,
,
∴阴影部分的面积为8 ![]() ﹣
﹣ ![]()
【解析】(1)连接OC,先证明∠OAC=∠OCA,进而得到OC∥AE,于是得到OC⊥CD,进而证明DE是⊙O的切线;(2)分别求出△OCD的面积和扇形OBC的面积,利用S阴影=S△COD﹣S扇形OBC即可得到答案.本题主要考查了切线的判定以及扇形的面积计算,解(1)的关键是证明OC⊥DE,解(2)的关键是求出扇形OBC的面积,此题难度一般.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了错题,从下列四个条件:
①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图所示),现有如下四种选法,你认为其中错误的是( )
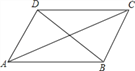
A. ①② B. ①③ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元。
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器5个以上超出部分按原价的七折销售。设购买个x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过5个,购买哪种品牌的计算器更合算?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.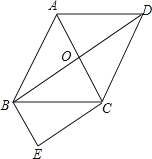
(1)求tan∠DBC的值;
(2)求证:四边形OBEC是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
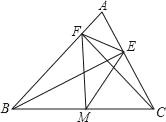
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)若EF=3,BC=8,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com