
【题目】若一个矩形的一边是另一边的两倍,则称这个矩形为方形.如图1,矩形![]() 中,
中,![]() ,则称
,则称![]() 为方形.
为方形.

(Ⅰ)设![]() 是方形的一组邻边,写出
是方形的一组邻边,写出![]() 的一组值为__________;
的一组值为__________;
(Ⅱ)在![]() 中,将
中,将![]() 分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使得这些矩形的边
分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使得这些矩形的边![]() 的对边分别在
的对边分别在![]() 上,如图2所示.
上,如图2所示.
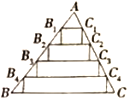
①若![]() ,
,![]() 边上的高为
边上的高为![]() ,判断以
,判断以![]() 为一边的矩形是否是方形?_________(填“是”或“否”);②若以
为一边的矩形是否是方形?_________(填“是”或“否”);②若以![]() 为一边的矩形为方形,则
为一边的矩形为方形,则![]() 与
与![]() 边上的高之比为__________.
边上的高之比为__________.
【答案】![]() 否
否 ![]() 或
或![]()
【解析】
(1)答案不唯一,根据已知举出即可;
(2)①求出△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,推出![]() ,
,![]() ,
,![]() ,
,![]() ,求出B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,MN=GN=GH=HE=4,B1Q=B2O=B3Z=B4K=4,根据已知判断即可;
,求出B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,MN=GN=GH=HE=4,B1Q=B2O=B3Z=B4K=4,根据已知判断即可;
②设AM=h,根据△ABC∽△AB3C3,得出![]() ,求出MN=GN=GH=HE=
,求出MN=GN=GH=HE=![]() h,分为两种情况:当B3C3=2×
h,分为两种情况:当B3C3=2×![]() h时,当B3C3=
h时,当B3C3=![]() ×
×![]() h时,代入求出即可.
h时,代入求出即可.
(1)答案不唯一,如a=1,b=2;
(2)①以B1C1为一边的矩形不是方形.
理由是:过A作AM⊥BC于M,交B1C1于E,交B2C2于H,交B3C3于G,交B4C4于N,则AM⊥B4C4,AM⊥B3C3,AM⊥B2C2,AM⊥B1C1,

∵由矩形的性质得:BC∥B1C1∥B2C2∥B3C3∥B4C4,
∴△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵AM=20,BC=25,
∴B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,
∴MN=GN=GH=HE=4,
∴B1Q=B2O=B3Z=B4K=4,
即B1C1≠2B1Q,B1Q≠2B1C1,
∴以B1C1为一边的矩形不是方形;
②∵以B3C3为一边的矩形为方形,设AM=h,
∴△ABC∽△AB3C3,
∴![]() ,
,
则AG=![]() h,
h,
∴MN=GN=GH=HE=![]() h,
h,
当B3C3=2×![]() h时,
h时,![]() ;
;
当B3C3=![]() h时,
h时,![]() .
.
综合上述:BC与BC边上的高之比是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知ABCD,点E是BC边上的一点,将边AD延长至点F,使∠AFC=∠DEC.

(1)求证:四边形DECF是平行四边形;
(2)若AB=13,DF=14,tan A=![]() ,求CF的长.
,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务.
三等分任意角问题是数学史上一个著名的问题,直到1837年,数学家才证明了“三等分任意角”是不能用尺规完成的.
在探索中,出现了不同的解决问题的方法
方法一:
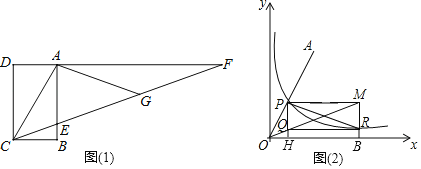
如图(1),四边形ABCD是矩形,F是DA延长线上一点,G是CF上一点,CF与AB交于点E,且∠ACG=∠AGC,∠GAF=∠F,此时∠ECB=![]() ∠ACB.
∠ACB.
方法二:
数学家帕普斯借助函数给出一种“三等分锐角”的方法(如图(2)):将给定的锐角∠AOB置于平面直角坐标系中,边OB在x轴上,边OA与函数y=![]() 的图象交于点P,以点P为圆心,以2OP长为半径作弧交图象于点R.过点P作x轴的平行线,过点R作y轴的平行线,两直线相交于点M,连接OM得到∠AOB,过点P作PH⊥x轴于点H,过点R作RQ⊥PH于点Q,则∠MOB=
的图象交于点P,以点P为圆心,以2OP长为半径作弧交图象于点R.过点P作x轴的平行线,过点R作y轴的平行线,两直线相交于点M,连接OM得到∠AOB,过点P作PH⊥x轴于点H,过点R作RQ⊥PH于点Q,则∠MOB=![]() ∠AOB.
∠AOB.
(1)在“方法一”中,若∠ACF=40°,GF=4,求BC的长.
(2)完成“方法二”的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,直线![]() 与x轴交于C点,与y轴交于点E,点A在x轴的负半轴,以A点为圆心,AO为半径的圆与直线的CE相切于点F,交x轴负半轴于另一点B.
与x轴交于C点,与y轴交于点E,点A在x轴的负半轴,以A点为圆心,AO为半径的圆与直线的CE相切于点F,交x轴负半轴于另一点B.
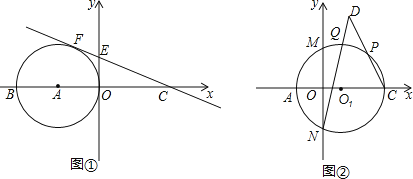
(1)求![]() 的半径;
的半径;
(2)连BF、AE,则BF与AE之间有什么位置关系?写出结论并证明.
(3)如图②,以AC为直径作![]() 交y轴于M,N两点,点P是弧MC上任意一点,点Q是弧PM的中点,连CP,NQ,延长CP,NQ交于D点,求CD的长.
交y轴于M,N两点,点P是弧MC上任意一点,点Q是弧PM的中点,连CP,NQ,延长CP,NQ交于D点,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时.数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速在l外取一点P,作PC⊥1,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°,测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速?(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )

A. 20 B. 24 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() ,与反比例函数
,与反比例函数![]() 交于点A(3,1)、B(-1,n),y1交y轴于点C,交x轴于点D.
交于点A(3,1)、B(-1,n),y1交y轴于点C,交x轴于点D.
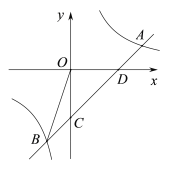
(1)求反比例函数及一次函数的解析式;
(2)求△OBD的面积;
(3)根据图象直接写出![]() >
>![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com