
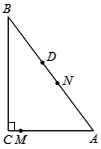
【题目】△ABC中,∠C=90°,点D在边AB上,AD=AC=7,BD=![]() BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
(1)求cosA的值.
(2)当以MN为直径的圆与△ABC一边相切时,求t的值.
【答案】(1)![]() ;(2)t=1或t=2.
;(2)t=1或t=2.
【解析】
试题(1)设BC=4m,AC=x,用m表示出AC和AB,根据三角函数定义即可求解.
(2)分⊙O与AB相切,⊙O与AC相切和⊙O与BC相切三种情况讨论即可.
(1)设BC=4m,AC=x,则BD=2m,AD=x,
∵![]() ,∴ 16
,∴ 16![]() +
+![]() =
=![]() . 解之得 x=3m.
. 解之得 x=3m.
从而AB=5m.
因此cosA=![]() .
.
(2)CM=t,AM=7-t,DN=2t,AN=7-2t,其中0≤t≤3.5,
记以MN为直径的圆为⊙O,当⊙O与AB相切时,则MN⊥AB,
因此![]()
![]() ,t=2,符合题意;
,t=2,符合题意;
当⊙O与AC相切时,则MN⊥AC,因此![]() ,t=-14,舍去;
,t=-14,舍去;
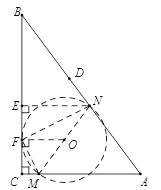
当⊙O与BC相切时,如图,作NE⊥BC,垂足为E.取EC的中点F,连结OF,则OF⊥BC,即点F为⊙O与BC相切的切点.连结MF,NF,则FM⊥FN,因此△FCM∽△NEF.
因此CM·EN=![]() .
.
而CM=t,EN=![]() ,EF=FC=
,EF=FC=![]() EC=
EC=![]() ,
,
因此![]() ,整理得
,整理得![]() ,解之得 t=1,t=-14(舍去) .
,解之得 t=1,t=-14(舍去) .
综上所得,当以MN为直径的圆与△ABC一边相切时,t=1或t=2.


科目:初中数学 来源: 题型:
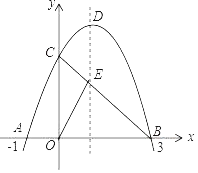
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,以BC为边向正方形内部作等边△BCE,连接AE并延长交CD于F,连接DE,下列结论:①AE=DE;②∠CEF=45°;③AE=EF;④△DEF∽△ABE,其中正确的结论共有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲16分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

查看答案和解析>>
科目:初中数学 来源: 题型:
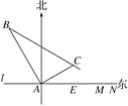
【题目】在某飞机场东西方向的地面l上有一长为1 km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5![]() 千米的C处.
千米的C处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
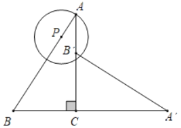
【题目】如图,△ABC中,∠ACB=90°,BC=3,cos∠B=![]() ,将△ABC绕点C顺时针旋转90°得到△AB'C,P为线段AB上的动点,以点P为圆心,PA长为半径作⊙P,当⊙P与△A′B′C的一边所在的直线相切时,⊙P的半径为_____.
,将△ABC绕点C顺时针旋转90°得到△AB'C,P为线段AB上的动点,以点P为圆心,PA长为半径作⊙P,当⊙P与△A′B′C的一边所在的直线相切时,⊙P的半径为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下公式:sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ;cos(α+β)=cosαcosβ﹣sinαsinβ,cos(α﹣β)=cosαcosβ+sinαsinβ;tan(α+β)=![]() (1﹣tanαtanβ≠0),合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值,如sin90°=sin(30°+60°)=sin30°cos60°+cos30°sin60°=
(1﹣tanαtanβ≠0),合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值,如sin90°=sin(30°+60°)=sin30°cos60°+cos30°sin60°=![]() =1,利用上述公式计算下列三角函数①sin105°=
=1,利用上述公式计算下列三角函数①sin105°=![]() ,②tan105°=﹣2﹣
,②tan105°=﹣2﹣![]() ,③sin15°=
,③sin15°=![]() ,④cos90°=0,其中正确的个数有( )
,④cos90°=0,其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
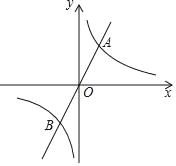
【题目】如图,已知正比例函数y=2x与反比例函数y=![]() (k>0)的图象交于A、B两点,且点A的横坐标为4.
(k>0)的图象交于A、B两点,且点A的横坐标为4.
(1)求k的值.
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com