
【题目】定义:若四边形中某个顶点与其它三个顶点的距离相等,则这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.
(1)判断:一个内角为120°的菱形 等距四边形.(填“是”或“不是”)
(2)如图,在5×5的网格图中有A、B两点,请在答题卷给出的两个网格图上各找出C、D两个格点,使得以A、B、C、D为顶点的四边形为互不全等的“等距四边形”,画出相应的“等距四边形”,并写出该等距四边形的端点均为非等距点的对角线长.


端点均为非等距点的对角线长为 端点均为非等距点的对角线长为
(3)如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连结AD,AC ,BC,若四边形ABCD是以A为等距点的等距四边形,求∠BCD的度数.

【答案】(1)是;(2)作图见解析, ![]() 或
或![]() (3)150°
(3)150°
【解析】试题分析:(1)根据菱形的性质和“等距四边形”的定义解答;
(2)根据“等距四边形”的定义作图,根据勾股定理求出对角线的长;
(3)根据等腰直角三角形的性质和“等距四边形”的定义以及三角形内角和定理、等腰三角形的性质计算即可.
试题解析:
(1)是

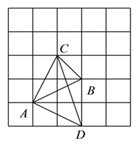
(2)端点非等距点的对角线长为![]()
点非等距点的对角线长为![]()
(3)连接BD,
∵△ABE与△CDE都是等腰直角三角形
∴DE=EC,AE=EB,
∠DEC+∠BEC=∠AEB+∠BEC即 ∠AEC=∠DEB
∴△AEC≌△BED
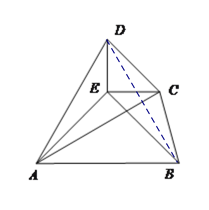
∴AC=BD
∵四边形ABCD是以A为等距点的等距四边形
∴AD=AB=AC
∴AD=AB=BD
∴△ABD是等边三角形
∴∠DAB=60°
∴∠DAE=∠DAB-∠EAB= 60°-45°=15°
∵AD=AC,DE=EC,AE=AE
∴△AED≌△AEC
∴∠CAE=∠DAE=15°
∴∠DAC=∠CAE+∠DAE=30°, ∠BAC=∠BAE-∠CAE=30°
∵AB=AC,AC=AD
∴![]() ,
,![]()
∴∠BCD=∠ACB+∠ACD=75°+75°=150°


科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=-x+4的图象与反比例![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)连接OA,OB,求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知l1⊥l2 , ⊙O与l1 , l2都相切,⊙O的半径为2cm,矩形ABCD的边AD、AB分别与l1 , l2重合,AB=4 ![]() cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s)
cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s) 
(1)如图①,连接OA、AC,则∠OAC的度数为°;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1 , A1 , C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<2时,求t的取值范围(解答时可以利用备用图画出相关示意图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年国庆节放假八天,高速公路免费通行,各地风景区游人如织,杭州西湖风景区累计接待游客超百万人次.据统计,
年国庆节放假八天,高速公路免费通行,各地风景区游人如织,杭州西湖风景区累计接待游客超百万人次.据统计, ![]() 月
月![]() 日的游客人数约为
日的游客人数约为![]() 万人,接下来的八天中每天游客人数变化如下表(正数表示比前一天多的人数,负数表示前一天少的人数):
万人,接下来的八天中每天游客人数变化如下表(正数表示比前一天多的人数,负数表示前一天少的人数):
日期 |
|
|
|
|
|
|
|
|
人数变化(万人) |
|
|
|
|
|
|
|
|
(![]() )
)![]() 万是__________(填“准确数”、“近似数”).
万是__________(填“准确数”、“近似数”).
(![]() )八天假期里,西湖景区游客最多的是
)八天假期里,西湖景区游客最多的是![]() 月__________日.
月__________日.
(![]() )
)![]() 月
月![]() 日西湖风景区接待游客多少万人?
日西湖风景区接待游客多少万人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com