
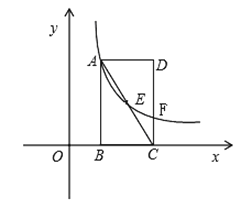
【题目】如图, 在直角坐标系中,长方形ABCD的边BC在X轴上,点B、D的坐标分别为B(1,0),D(3,3).
(1)直接写出点A、点C的坐标:A: C: ;
(2)若反比例函数![]() 的图象经过直线AC上的点E,且点E的坐标为(2,m),求
的图象经过直线AC上的点E,且点E的坐标为(2,m),求![]() 的值及反比例函数的解析式;
的值及反比例函数的解析式;
(3)若(2)中的反比例函数的图象与CD相交于点F,连接 EF,在线段AB上(端点除外)找一点P,使得:S△PEF=S△cEF,并求出点P的坐标.
【答案】(1)C(3,0)(2)3/2,![]() (3)(1,1)
(3)(1,1)
【解析】
解:(1)C(3,0)………………………………………(3分)
(2)设直线AC的解析式为![]() ,则
,则
![]() ,解得:
,解得: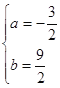
∴直线AC的解析式为![]() …………………………………………………(4分)
…………………………………………………(4分)
∵点E(2,m)在直线AC上
∴![]()
∴![]() ……………………(5分)
……………………(5分)
∵反比例函数y=![]() 的图象经过点E
的图象经过点E
∴![]()
∴反比例函数的解析式为![]() ……………………………………………………(7分)
……………………………………………………(7分)
(3)在![]() 中,当
中,当![]() 时,
时,![]() ∴
∴![]() ………………………………(8分)
………………………………(8分)
过点C作直线PC∥EF交AB于P,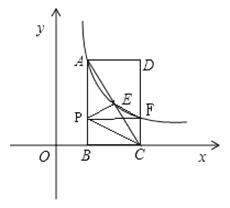
则![]() ………………………(9分)
………………………(9分)
设直线EF的解析式为![]()
∴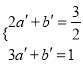 解得:
解得: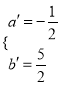 ∴
∴![]() ……………(10分)
……………(10分)
设直线PC的解析式为![]() ,并把C(3,0)代入得:
,并把C(3,0)代入得:![]()
∴![]() …………………………………………………………………(12分)
…………………………………………………………………(12分)
当![]() 时,y=1 ∴点P(1,1) ………………………………………(13分)
时,y=1 ∴点P(1,1) ………………………………………(13分)
(1)由D点坐标得
(2)求出直线AC的解析式,把E的坐标代入求出m的值,从而求得反比例函数的解析式
(3)过点C作直线PC∥EF交AB于P,求出直线EF的解析式,得出直线PC的解析式,从而求出点P的坐标


科目:初中数学 来源: 题型:
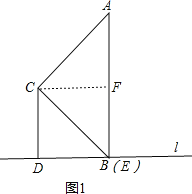
【题目】在△ABC中,∠ACB=90°,经过点B的直线l(不与直线AB重合)与直线BC的夹角等于∠ABC,分别过点C、点A作直线l的垂线,垂足分别为点D、点E.
(1)如图1,当点E与点B重合时,若AE=4,判断以C点为圆心CD长为半径的圆C与直线AB的位置关系并说明理由;
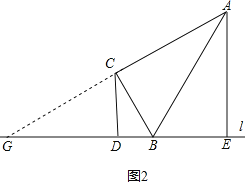
(2)如图2,当点E在DB延长线上时,求证:AE=2CD;
(3)记直线CE与直线AB相交于点F,若,![]() ,CD=4,求BD的长.
,CD=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
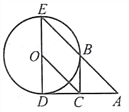
【题目】如图,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于点B,且四边形BCOE是平行四边形。
(1)BC是⊙O的切线吗?若是,给出证明:若不是,请说明理由;
(2)若⊙O半径为1,求AD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入表示它所在的数集的大括号:
﹣2.4,3,21.08,0,﹣100,﹣(﹣2.28),![]() ,﹣|﹣4|,
,﹣|﹣4|,
正有理数集合:{ }
负有理数集合:{ }
整数集合:{ }
分数集合:{ }.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数
3,9,27,81…①
1,3,9,27…②
2,10,26,82…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)设x,y,z分别为第①②③ 行的2019个数,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一种产品去年的产量是100万件,计划明年产量达到121万件,假设去年到明年这种产品产量的年增长率相同。
(1)求去年到明年这种产品产量的年增长率;
(2)今年这种产品的产量应达到多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
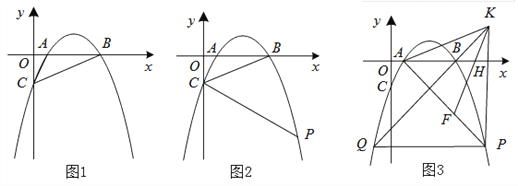
【题目】在平面直角坐标系中,抛物线![]() 与x轴交于A、B(A点在B点的左侧)与y轴交于点C。
与x轴交于A、B(A点在B点的左侧)与y轴交于点C。
(1)如图1,连接AC、BC,求△ABC的面积。
(2)如图2:
①过点C作CR∥x轴交抛物线于点R,求点R的坐标;
②点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的坐标。
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=![]() ,连接KB并延长交抛物线于点Q,求PQ的长。
,连接KB并延长交抛物线于点Q,求PQ的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过点(3,2)和(1,4).
(1)画出此函数的图象;
(2)求此一次函数的表达式;
(3)若此函数的图象与x轴交于点A,与y轴交于点B,求线段AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com