精英家教网 > 初中数学 > 题目详情

我校数学活动小组在完成测量校内路灯高度后，填写了如下《数学活动报告》中附件的一部分．请你根据以下图示及有关数据，完成未完成的部分：

课　　题

测量校内路灯的高度

示
意
图

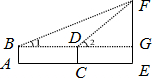测得数据

AB=1.6m，AC=2m，∠1=30°，∠2=45°

计
算
过
程

参考数据

≈1.414，

≈1.732

结论
（精确到0.1m）

EF=

4.3

分析：此题涉及两个直角三角形，根据题意，利用公共边即GF的特殊位置，解两个直角三角形，可得答案．

解答：解：在Rt△FDG中，
∵∠2=45°，
∴FG=DG
设FG=DG=x，
则BG=2+x，
Rt△BFG中，FG=BG•tan∠1
即：x=

（x+2）．
解得：x=

+1≈2.7m
∴EF=FG+GE=2.7+1.6=4.3

点评：本题考查了解直角三角形的应用，要求学生能借助仰角构造直角三角形并结合图形利用三角函数解直角三角形．

练习册系列答案

贵州专版寒假作业吉林人民出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

（2013•南昌）某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：
（1）操作发现：在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是

①②③④

（填序号即可）
①AF=AG=

AB；②MD=ME；③整个图形是轴对称图形；④MD⊥ME．
（2）数学思考：在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD和ME具有怎样的数量关系？请给出证明过程；
（3）类比探究：
（i）在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，试判断△MED的形状．答：

等腰直角三角形

．
（ii）在三边互不相等的△ABC中（见备用图），仍分别以AB和AC为斜边，向△ABC的内侧作（非等腰）直角三角形ABD和（非等腰）直角三角形ACE，M是BC的中点，连接MD和ME，要使（2）中的结论此时仍然成立，你认为需增加一个什么样的条件？（限用题中字母表示）并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

我校数学活动小组在完成测量校内路灯高度后，填写了如下《数学活动报告》中附件的一部分．请你根据以下图示及有关数据，完成未完成的部分：
课　　题测量校内路灯的高度
示
意
图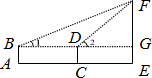
测得数据 AB=1.6m，AC=2m，∠1=30°，∠2=45°
计
算
过
程

参考数据 $数学公式$ ， $数学公式$
结论
（精确到0.1m） EF=________m

查看答案和解析>>

科目：初中数学 来源：湖南省月考题 题型：解答题

我校数学活动小组在完成测量校内路灯高度后，填写了如下《数学活动报告》中附件的一部分．请你根据以下图示及有关数据，完成未完成的部分：

查看答案和解析>>

科目：初中数学 来源：2007年广东省汕尾市陆丰市玉燕中学中考数学模拟试卷（2月份）（解析版） 题型：解答题

我校数学活动小组在完成测量校内路灯高度后，填写了如下《数学活动报告》中附件的一部分．请你根据以下图示及有关数据，完成未完成的部分：

课题	测量校内路灯的高度
示意图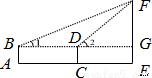
测得数据	AB=1.6m，AC=2m，∠1=30°，∠2=45°
计算过程
参考数据	，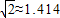
结论（精确到0.1m）	EF=______m

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学