
【题目】如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=10,AB=8
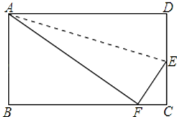
求.(1)FC的长
(2)EC的长.
【答案】(1)4;(2)3
【解析】
(1)由矩形的性质可得AD=BC=10,∠B=90°,根据折叠可得AD=AF=10,再利用勾股定理可得BF长,进而可得FC长;
(2)根据矩形的性质可得AB=CD=8,∠C=90°,设ED=x,则EF=x,EC=8﹣x,再在Rt△EFC利用勾股定理可得方程x2=(8﹣x)2+42,解出x的值,进而可得EC长.
解:(1)根据折叠可得AD=AF,
∵四边形ABCD是矩形,
∴AD=BC=10,∠B=90°,
∴AF=10,
∴BF=![]() ,
,
∴FC=4;
(2)根据折叠可得ED=EF,
∵四边形ABCD是矩形,
∴AB=CD=8,∠C=90°,
设ED=x,则EF=x,EC=8﹣x,
在Rt△EFC中,EF2=EC2+FC2,
x2=(8﹣x)2+42,
解得:x=5,
∴EC=8﹣5=3.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】有一个矩形铁片,长是![]() ,宽是
,宽是![]() ,中间挖去
,中间挖去![]() 的矩形,剩下的铁框四周一样宽,若设宽度为
的矩形,剩下的铁框四周一样宽,若设宽度为![]() ,那么挖去的矩形长是________
,那么挖去的矩形长是________![]() ,宽是________
,宽是________![]() ,根据题意可得方程________.
,根据题意可得方程________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于C、H.请判断下列结论:(1)BE=DF;(2)AG=GH=HC;(3)EG=![]() BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
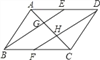
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发沿
点出发沿![]() 路径向终点运动,终点为
路径向终点运动,终点为![]() 点,点
点,点![]() 从
从![]() 点出发沿
点出发沿![]() 路径向终点运动,终点为
路径向终点运动,终点为![]() 点,点
点,点![]() 和
和![]() 分别以每秒
分别以每秒![]() 和
和![]() 的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过
的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过![]() 和
和![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .设运动时间为
.设运动时间为![]() 秒,要使以点
秒,要使以点![]() ,
,![]() ,
,![]() 为顶点的三角形与以点
为顶点的三角形与以点![]() ,
,![]() ,
,![]() 为顶点的三角形全等,则
为顶点的三角形全等,则![]() 的值为______.
的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥享有“中国淡水龙虾之都”的美称.甲乙两家小龙虾美食店,平时以同样的价格出售品质相同的小龙虾,“龙虾节”期间,甲乙两家店都让利酬宾,在人数不超过20人的前提下,付款金额y甲,y乙(单位元)与人数之间的函数关系如图所示.

(1)直接写出y甲,y乙关于x的函数关系式.
(2)小王公司想在“龙虾节”期间组织团建,在甲乙两家店就餐,如何选择甲乙两家美食店吃小龙虾更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 、
、![]() 、
、![]() 为矩形的四个顶点,
为矩形的四个顶点,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 以
以![]() 的速度向点
的速度向点![]() 移动,一直到达
移动,一直到达![]() 为止,点
为止,点![]() 以
以![]() 的速度向
的速度向![]() 移动.
移动.

(1)![]() 、
、![]() 两点从出发开始到几秒时四边形
两点从出发开始到几秒时四边形![]() 是矩形?
是矩形?
(2)![]() 、
、![]() 两点从出发开始到几秒时,点
两点从出发开始到几秒时,点![]() 和点
和点![]() 的距离是
的距离是![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com